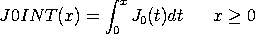J0INT
Name:
Type:
Purpose:
This program computes the integral of the Bessel function
J0(x).
Description:
The J0INT function is defined as:
with J0 denoting the Bessel function of the
first kind of order 0.
Dataplot computes this function using ACM Algorithm 757 (see
Reference: below). The function is computed using Chebyshev
expansions, the coefficients of which are given to 20 decimal
places.
Syntax:
LET <y> = J0INT(<x>)
<SUBSET/EXCEPT/FOR qualification>
where <x> is a non-negative number, variable or
parameter;
<y> is a variable or a parameter (depending on what
<x> is) where the computed J0INT function
values are stored;
and where the <SUBSET/EXCEPT/FOR qualification> is optional.
Examples:
LET A = J0INT(2.3)
PLOT J0INT(X) FOR X = 0 .01 10
LET X2 = J0INT(X1) FOR X1 = 0.1 0.1 3.0
Default:
Synonyms:
Related Commands:
|
BESSJ0
|
= Compute the Bessel function of the first kind and
order 0.
|
|
BESSJ1
|
= Compute the Bessel function of the first kind and
order 1.
|
|
BESSJN
|
= Compute the Bessel function of the first kind and
order N.
|
|
BESSIN
|
= Compute the modified Bessel function of the first
kind and order N.
|
|
BESSKN
|
= Compute the modified Bessel function of the third
kind and order N.
|
|
BESSYN
|
= Compute the Bessel function of the second kind and
order N.
|
|
I0INT
|
= Compute the integral of the modified Bessel function
of the first kind and order 0.
|
|
K0INT
|
= Compute the integral of the modified Bessel function
of the third kind and order 0.
|
|
Y0INT
|
= Compute the integral of the Bessel function of the
second kind and order 0.
|
Reference:
"ACM Transactions of Mathematical Software", Allan MacLead,
Vol. 22, No. 3, September, 1996, pp. 288-301.
Applications:
Implementation Date:
Program:
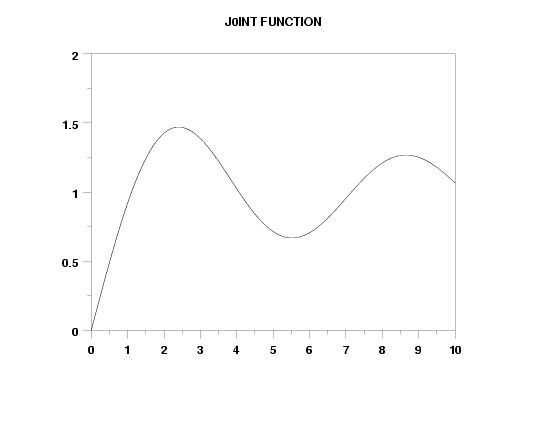
TITLE J0INT FUNCTION
PLOT J0INT(X) FOR X = 0 0.01 10
Date created: 11/7/2005
Last updated: 11/7/2005
Please email comments on this WWW page to
alan.heckert@nist.gov.
|