LOG ODDS RATIO STANDARD ERROR

LOG ODDS RATIO STANDARD ERROR (LET)

Let Subcommand

Compute the standard error of the bias corrected log odds ratio between two binary variables.

Given two variables where each variable has exactly two possible outcomes (typically defined as success and failure), we define the odds ratio as:
o = (N₁₁/N₁₂)/ (N₂₁/N₂₂)
    = (N₁₁N22)/ (N₁₂N₂₁)

where

N₁₁ = number of successes in sample 1
N₂₁ = number of failures in sample 1
N₁₂ = number of successes in sample 2
N₂₂ = number of failures in sample 2


The first definition shows the meaning of the odds ratio clearly, although it is more commonly given in the literature with the second definition.

The log odds ratio is the logarithm of the odds ratio:

l(o) = LOG{(N₁₁/N₁₂)/ (N₂₁/N₂₂)}
       = LOG{(N₁₁N22)/ (N₁₂N₂₁)}

Success and failure can denote any binary response. Dataplot expects "success" to be coded as "1" and "failure" to be coded as "0".

Dataplot actually returns the bias corrected version of the statistic:

l'(o) = LOG[{(N₁₁+0.5) (N₂₂+0.5)}/ {(N₁₂+0.5) (N₂₁+0.5)}]

In addition to reducing bias, this statistic also has the advantage that the odds ratio is still defined even when N₁₂ or N₂₁ is zero (the uncorrected statistic will be undefined for these cases).

The standard error of this bias corrected log odds ratio is then

\[ \hat{SE}(l'(o)) = \sqrt{\frac{1}{n_{11} + 0.5} + \frac{1}{n_{21}+ 0.5} + \frac{1}{n_{12}+0.5} + \frac{1}{n_{22}+0.5}} \]

LET <par> = LOG ODDS RATIO STANDARD ERROR <y1> <y2>
                        <SUBSET/EXCEPT/FOR qualification>
where <y1> is the first response variable;
            <y2> is the second response variable;
            <par> is a parameter where the computed log odds ratio standard error is stored;
and where the <SUBSET/EXCEPT/FOR qualification> is optional.

LET A = LOG ODDS RATIO STANDARD ERROR Y1 Y2
LET A = LOG ODDS RATIO STANDARD ERROR Y1 Y2 SUBSET TAG > 2

The two variables need not have the same number of elements.

There are two ways you can define the response variables:
1. Raw data - in this case, the variables contain 0's and 1's.

   If the data is not coded as 0's and 1's, Dataplot will check for the number of distinct values. If there are two distinct values, the minimum value is converted to 0's and the maximum value is converted to 1's. If there is a single distinct value, it is converted to 0's if it is less than 0.5 and to 1's if it is greater than or equal to 0.5. If there are more than two distinct values, an error is returned.

2. Summary data - if there are two observations, the data is assummed to be the 2x2 summary table. That is,
   Y1(1) = N11
   Y1(2) = N21
   Y2(1) = N12
   Y2(2) = N22
   

The following additional commands are supported
TABULATE LOG ODDS RATIO STANDARD ERROR Y1 Y2 X
CROSS TABULATE LOG ODDS RATIO STANDARD ERROR ...
            Y1 Y2 X1 X2

LOG ODDS RATIO STANDARD ERROR PLOT Y1 Y2 X
CROSS TABULATE LOG ODDS RATIO STANDARD ERROR PLOT ...
            Y1 Y2 X1 X2

BOOTSTRAP LOG ODDS RATIO STANDARD ERROR PLOT Y1 Y2
JACKNIFE LOG ODDS RATIO STANDARD ERROR PLOT Y1 Y2


Note that the above commands expect the variables to have the same number of observations. If the two samples are in fact of different sizes, there are two ways to address the issue:

1. Y1 and Y2 can contain the summary data. That is,
   Y1(1) = N11
   Y1(2) = N21
   Y2(1) = N12
   Y2(2) = N22
   

   This is a useful option in that the data is sometimes only available in summary form. Note that this will not work for the BOOTSTRAP PLOT and JACKNIFE PLOT commands (these require raw data).

2. You can specify a missing value for the smaller sample. For example, if Y1 has 100 observations and Y2 has 200 observations, you can do something like
   SET STATISTIC MISSING VALUE -99
   LET Y1 = -99 FOR I = 101 1 200
   

None

LOGIT STANDARD ERROR
STANDARD ERROR LOG ODDS RATIO
STANDARD ERROR LOGIT

LOG ODDS RATIO	= Compute the bias corrected log odds ratio
ODDS RATIO	= Compute the bias corrected odds ratio
ODDS RATIO STANDARD ERROR	= Compute the standard error of the bias corrected odds ratio
TRUE POSITIVES	= Compute the proportion of true positives.
TRUE NEGATIVES	= Compute the proportion of true negatives.
FALSE NEGATIVES	= Compute the proportion of false negatives.
FALSE POSITIVES	= Compute the proportion of false positives.
TEST SENSITIVITY	= Compute the test sensitivity.
TEST SPECIFICITY	= Compute the test specificity.
RELATIVE RISK	= Compute the relative risk.
STATISTICS PLOT	= Generate a statistic versus subset plot.
BOOTSTRAP PLOT	= Generate a bootstrap plot.
TABULATE	= Perform a tabulation for a specified statistic.

Fleiss, Levin, and Paik (2003), "Statistical Methods for Rates and Proportions," Third Edition, Wiley, chapter 6.

Categorical Data Analysis

2007/05

 
let n = 1
.
let p = 0.2
let y1 = binomial rand numb for i = 1 1 100
let p = 0.1
let y2 = binomial rand numb for i = 1 1 100
.
let p = 0.4
let y1 = binomial rand numb for i = 101 1 200
let p = 0.08
let y2 = binomial rand numb for i = 101 1 200
.
let p = 0.15
let y1 = binomial rand numb for i = 201 1 300
let p = 0.18
let y2 = binomial rand numb for i = 201 1 300
.
let p = 0.6
let y1 = binomial rand numb for i = 301 1 400
let p = 0.45
let y2 = binomial rand numb for i = 301 1 400
.
let p = 0.3
let y1 = binomial rand numb for i = 401 1 500
let p = 0.1
let y2 = binomial rand numb for i = 401 1 500
.
let x = sequence 1 100 1 5
.
let a = log odds ratio standard error y1 y2 subset x = 1
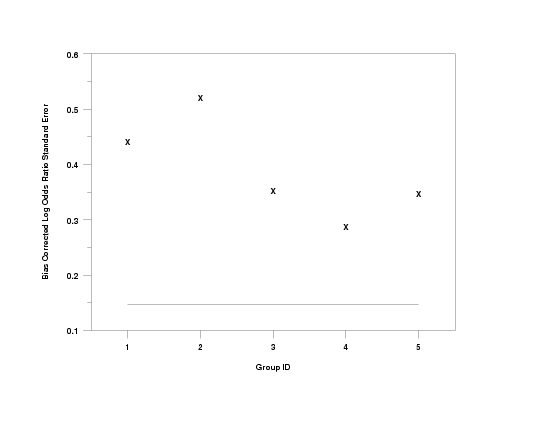
tabulate log odds ratio standard error y1 y2 x
.
label case asis
xlimits 1 5
major xtic mark number 5
minor xtic mark number 0
xtic mark offset 0.5 0.5
y1label Bias Corrected Log Odds Ratio Standard Error
x1label Group ID
character x blank
line blank solid
.
log odds ratio standard error plot y1 y2 x