SED navigation bar go to SED home page go to Dataplot home page go to NIST home page SED Home Page SED Staff SED Projects SED Products and Publications Search SED Pages
Dataplot Vol 2 Vol 1

LSNCDF

Name:
    LSNCDF (LET)
Type:
    Library Function
Purpose:
    Compute the log-skew-normal cumulative distribution function.
Description:
    The log-skew-normal distribution can be defined in terms of the skew-normal distribution as follows:

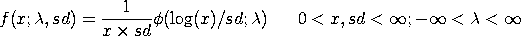
      f(x,lambda,sd)=(1/(sd*x))*phi(LOG(x)/sd;lambda) 0 < x, sd < infinity; -infinity < lambda < infinity

    with lambda denoting the skewness parameter, sd denoting the standard deviation of the corresponding normal distribution, and phi(x;lambda denoting the probability density of the skew normal distribution.

    This is analogous to how the lognormal distribution is defined in terms of the normal distribution. If lamba = 0, the log-skew-normal distribution reduces to the lognormal distributiion.

    The log-skew-normal cumulative distribution is computed by numerically integrating the probability density function.

    The standard log-skew-normal distribution can be generalized with location and scale parameters in the usual way.

Syntax:
    LET <y> = LSNCDF(<x>,<lambda>,<sd>,<loc>,<scale>)
                            <SUBSET/EXCEPT/FOR qualification>
    where <x> is a variable or a parameter;
                <lambda> is a number of parameter that specifies the value of the skewness shape parameter;
                <sd> is a number of parameter that specifies the value of the sd shape parameter;
                <loc> is a number of parameter that specifies the value of the location parameter;
                <scale> is a number of parameter that specifies the value of the scale parameter;
                <y> is a variable or a parameter (depending on what <x> is) where the computed log-skew-normal cdf value is stored;
    and where the <SUBSET/EXCEPT/FOR qualification> is optional.

    Note that the location and scale parameters are optional.

Examples:
    LET A = LSNCDF(3,1,1)
    LET A = LSNCDF(A1,LAMBDA,SD)
    LET X2 = LSNCDF(X1,0.5,1.5)
Default:
    None
Synonyms:
    None
Related Commands:
    LSNPDF = Compute the log-skew-normal probability density function.
    LSNPPF = Compute the log-skew-normal percent point function.
    SNPDF = Compute the skew-normal probability density function.
    NORPDF = Compute the normal density function.
    LGNPDF = Compute the lognormal density function.
    CHIPDF = Compute the chi probability density function.
    CHSPDF = Compute the chi-square probability density function.
    WEIPDF = Compute the Weibull probability density function.
Reference:
    "Log-Skew-Normal and Log-Skew-t Distributions as Models for Family Income Data", Azzalini, Dal Cappello, and Kotz, Journal of Income Distribution, Vol. 11, No. 3-4, 2003, pp. 12-20.

    "A Class of Distributions Which Includes the Normal Ones", Azzalini, Scandinavian Journal of Statistics, 12, 171-178.

    "Continuous Univariate Distributions: Volume I", Second Edition, Johnson, Kotz, and Balakrishnan, Wiley, 1994, p. 454.

Applications:
    Distributional Modeling
Implementation Date:
    3/2004
Program: 
     
Y1LABEL Probability
X1LABEL X
LABEL CASE ASIS
X1LABEL DISPLACEMENT 12
Y1LABEL DISPLACEMENT 12
MULTIPLOT 2 2
MULTIPLOT CORNER COORDINATES 0 0 100 100
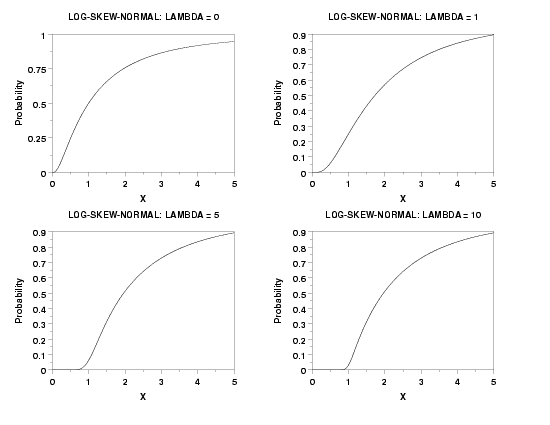
TITLE LOG-SKEW-NORMAL: LAMBDA = 0
PLOT LSNCDF(X,0) FOR X = 0.01  0.01  5
TITLE LOG-SKEW-NORMAL: LAMBDA = 1
PLOT LSNCDF(X,1) FOR X = 0.01  0.01  5
TITLE LOG-SKEW-NORMAL: LAMBDA = 5
PLOT LSNCDF(X,5) FOR X = 0.01  0.01  5
TITLE LOG-SKEW-NORMAL: LAMBDA = 10
PLOT LSNCDF(X,10) FOR X = 0.01  0.01  5
END OF MULTIPLOT
    plot generated by sample program

Date created: 7/7/2004
Last updated: 7/7/2004
Please email comments on this WWW page to alan.heckert@nist.gov.