SED navigation bar go to SED home page go to Dataplot home page go to NIST home page SED Home Page SED Staff SED Projects SED Products and Publications Search SED Pages
Dataplot Vol 2 Vol 1

LSTCDF

Name:
    LSTCDF (LET)
Type:
    Library Function
Purpose:
    Compute the log-skew-t cumulative distribution function.
Description:
    The log-skew-t distribution has the following probability density function:

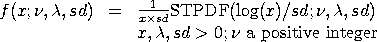
      f(x,nu,lambda,sd)=(1/(sd*x))**STPDF(LOG(x)/sd,nu,lambda,sd) x, lambda, sd > 0; nu a positive integer

    with STPDF denoting the skew-t distribution (enter HELP STPDF for details) and lambda, nu, and sd denoting the shape parameters.

    The cumulative distribution function is computed by numerically integrating the log-skew-t probability density function.

    For lambda = 0, the log-skew-t reduces to a log-t distribution.

    The standard log-skew-t distribution can be generalized with location and scale parameters in the usual way.

Syntax:
    LET <y> = LSTCDF(<x>,<nu>,<lambda>,<sd>,<loc>,<scale>)
                            <SUBSET/EXCEPT/FOR qualification>
    where <x> is a variable or a parameter;
                <nu> is a number of parameter that specifies the value of the degrees of freedom shape parameter;
                <lambda> is a number of parameter that specifies the value of the skewness shape parameter;
                <sd> is a number or parameter that specifies the value of the standard deviation parameter;
                <loc> is a number or parameter that specifies the value of the location parameter;
                <scale> is a number or parameter that specifies the value of the scale parameter;
                <y> is a variable or a parameter (depending on what <x> is) where the computed log-skew-t cdf value is stored;
    and where the <SUBSET/EXCEPT/FOR qualification> is optional.

    Note that the location and scale parameters are optional.

Examples:
    LET A = LSTCDF(3,5,1,2)
    LET A = LSTCDF(A1,DF,LAMBDA,2)
    PLOT LSTCDF(X,NU,LAMBDA,SD) FOR X = 0.01 0.01 10
Default:
    None
Synonyms:
    None
Related Commands:
    LSTPDF = Compute the log-skew-t probability density function.
    LSTPPF = Compute the log-skew-t percent point function.
    STPDF = Compute the skew-t probability density function.
    SNPDF = Compute the skew-normal probability density function.
    TPDF = Compute the t probability density function.
    FTPDF = Compute the folded t probability density function.
    NORPDF = Compute the normal density function.
    CHSPDF = Compute the chi-square probability density function.
Reference:
    "A Class of Distributions Which Includes the Normal Ones", Azzalini, Scandinavian Journal of Statistics, 12, 171-178.

    "Log-Skew-Normal and Log-Skew-t Distributions as Models for Family Income Data", Azzalini, Dal Cappello, and Kotz, Journal of Income Distribution, Vol. 11, No. 3-4, 2003, pp. 12-20.

Applications:
    Distributional Modeling
Implementation Date:
    1/2004
Program: 
     
Y1LABEL Probability
X1LABEL X
LABEL CASE ASIS
X1LABEL DISPLACEMENT 12
Y1LABEL DISPLACEMENT 12
MULTIPLOT 2 2
MULTIPLOT CORNER COORDINATES 0 0 100 100
LET SD = 1
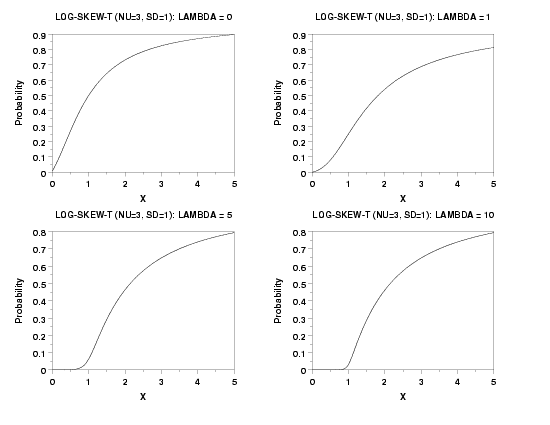
TITLE LOG-SKEW-T (NU=3, SD=1): LAMBDA = 0
PLOT LSTCDF(X,3,0,SD) FOR X = 0.01  0.01  5
TITLE LOG-SKEW-T (NU=3, SD=1): LAMBDA = 1
PLOT LSTCDF(X,3,1,SD) FOR X = 0.01 0.01  5
TITLE LOG-SKEW-T (NU=3, SD=1): LAMBDA = 5
PLOT LSTCDF(X,3,5,SD) FOR X = 0.01  0.01  5
TITLE LOG-SKEW-T (NU=3, SD=1): LAMBDA = 10
PLOT LSTCDF(X,3,10,SD) FOR X = 0.01  0.01  5
END OF MULTIPLOT
    plot generated by sample program

Date created: 7/7/2004
Last updated: 7/7/2004
Please email comments on this WWW page to alan.heckert@nist.gov.