MCLPDF

MCLPDF (LET)

Library Function

Compute the McLeish probability density function.

The standard form of the McLeish distribution has the following probability density function:

with K(.) denoting the modified Bessel function of the of the second kind of order and denoting the gamma function.

The standard McLeish distribution can be generalized with location and scale parameters in the usual way.

LET <y> = MCLPDF(<x>,<alpha>,<loc>,<scale>)
                        <SUBSET/EXCEPT/FOR qualification>
where <x> is a variable, a number, or a parameter;
            <alpha> is a positive number of parameter that specifies the value of the shape parameter;
            <loc> is an optional number or parameter that specifies the value of the location parameter;
            <scale> is an optional positive number or parameter that specifies the value of the scale parameter;
            <y> is a variable or a parameter (depending on what <x> is) where the computed McLeish pdf value is stored;
and where the <SUBSET/EXCEPT/FOR qualification> is optional.

LET Y = MCLPDF(3,1.5)
LET Y = MCLPDF(X1,ALPHA)
PLOT MCLPDF(X,ALPHA) FOR X = -10 0.01 10

DATAPLOT uses the routine BESK from the SLATEC Common Mathematical Library to compute the modified Bessel function of the third kind. SLATEC is a large set of high quality, portable, public domain Fortran routines for various mathematical capabilities maintained by seven federal laboratories.

To generate McLeish random numbers, enter the commands
LET ALPHA = <value>
LET Y = MCLEISH RANDOM NUMBERS FOR I = 1 1 N


To generate a McLeish probability plot or a McLeish Kolmogorov-Smirnov or chi-square goodness of fit test, enter the following commands

LET ALPHA = <value>
MCLEISH PROBABILITY PLOT Y
MCLEISH KOLMOGOROV SMIRNOV GOODNESS OF FIT Y
MCLEISH CHI-SQUARE GOODNESS OF FIT Y


To generate a PPCC or Kolmogorov-Smirnov plot, enter the following commands

LET ALPHA1 = <value>
LET ALPHA2 = <value>
MCLEISH PPCC PLOT Y
MCLEISH KS PLOT Y


The default values for ALPHA1 and ALPHA2 are 1.0 and 15.5.

For the McLeish distribution, the shape parameter acts a bit like a scale parameter. For this reason, the KS PLOT with the location and scale parameters fixed will probably work better than the PPCC PLOT. One recommendation is to set the scale parameter to 1 and the location parameter to the mode of the data (the McLeish distribution is symmetric). You can use the relative histogram or the kernel density plot to determine a useful value for the location. For example,

LET KSLOC = 0
LET KSSCALE = 1
MCLEISH KS PLOT Y

None

None

MCLCDF	= Compute the McLeish cumulative distribution function.
MCLPPF	= Compute the McLeish percent point function.
GMCPDF	= Compute the generalized McLeish probability density function.
GALPDF	= Compute the generalized asymmetric Laplace probability density function.
GIGPDF	= Compute the generalized inverse Gaussian probability density function.
BEIPDF	= Compute the Bessel I-function probability density function.
BEKPDF	= Compute the Bessel K-function probability density function.

Johnson, Kotz, and Balakrisnan, "Continuous Univariate Distributions--Volume I", Second Edition, Wiley, 1994, pp. 50-53.

Distributional Modeling

8/2004

 
Y1LABEL Probability
X1LABEL X
LABEL CASE ASIS
TITLE CASE ASIS
CASE ASIS
Y1LABEL DISPLACEMENT 12
MULTIPLOT 2 2
MULTIPLOT CORNER COORDINATES 0 0 100 95
MULTIPLOT SCALE FACTOR 2
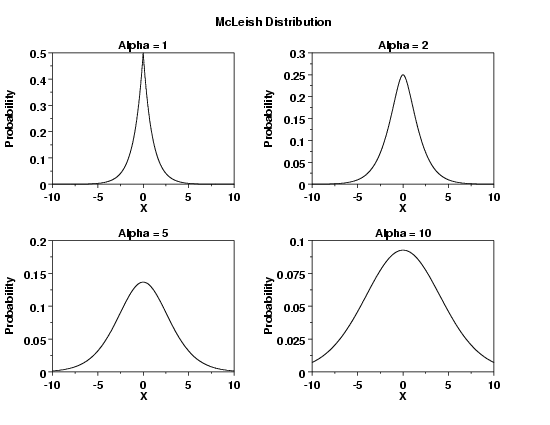
TITLE Alpha = 1
PLOT MCLPDF(X,1) FOR X = -10  0.01 10
TITLE Alpha = 2
PLOT MCLPDF(X,2) FOR X = -10  0.01 10
TITLE Alpha = 5
PLOT MCLPDF(X,5) FOR X = -10  0.01 10
TITLE Alpha = 10
PLOT MCLPDF(X,10) FOR X = -10  0.01 10
END OF MULTIPLOT
MOVE 50 97
JUSTIFICATION CENTER
TEXT McLeish Distribution