MUTPPF

MUTPPF (LET)

Library Function

Compute the Muth percent point function with shape parameter .

The standard Muth distribution has the following cumulative distribution function:

with denoting the shape parameter.

The percent point function is computed by numerically inverting the cumulative distribution function using a bisection method.

This distribution can be generalized with location and scale parameters in the usual way using the relation

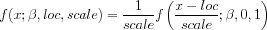
with <loc> and <scale> denoting the location and scale parameters, respectively.

LET <y> = MUTPPF(<p>,<beta>,<loc>,<scale>)
                        <SUBSET/EXCEPT/FOR qualification>
where <p> is a number, parameter, or variable in the interval [0,1];
            <y> is a variable or a parameter (depending on what <p> is) where the computed Muth ppf value is stored;
            <beta> is a number, parameter, or variable that specifies the shape parameter;
            <loc> is a number, parameter, or variable that specifies the location parameter;
            <scale> is a positive number, parameter, or variable that specifies the scale parameter;
and where the <SUBSET/EXCEPT/FOR qualification> is optional.

If <loc> and <scale> are omitted, they default to 0 and 1, respectively.

LET A = MUTPPF(0.95,0.2)
LET Y = MUTPPF(P,0.5,0,5)
PLOT MUTPPF(P,0.7,0,3) FOR P = 0.01 0.01 0.99

None

None

MUTCDF	= Compute the Muth cumulative distribution function.
MUTCHAZ	= Compute the Muth cumulative hazard function.
MUTHAZ	= Compute the Muth hazard function.
MUTPDF	= Compute the Muth probability density function.
RAYPDF	= Compute the Rayleigh probability density function.
WEIPDF	= Compute the Weibull probability density function.
LGNPDF	Compute the lognormal probability density function.
EXPPDF	= Compute the exponential probability density function.
LOGPDF	= Compute the logistic probability density function.
GAMPDF	= Compute the gamma probability density function.
EWEPDF	= Compute the exponentiated Weibull probability density function.
B10PDF	= Compute the Burr type 10 probability density function.

Leemis and McQuestion (2008), "Univariate Distribution Relationships", The American Statistician, Vol. 62, No. 1, pp. 45-53.

Muth (1977), "Reliability Models with Positive Memory Derived from the Mean Residual Life Function", in The Theory and Applications of Reliability, Eds. Tsokos and Shimi, New York: Academic Press Inc., pp. 401-435.

Distributional Modeling

2008/2

LABEL CASE ASIS
TITLE CASE ASIS
TITLE OFFSET 2
.
MULTIPLOT 2 2
MULTIPLOT CORNER COORDINATES 0 0 100 95
MULTIPLOT SCALE FACTOR 2
.
LET BETA  = 0.2
TITLE BETA = ^BETA
PLOT MUTPPF(P,BETA) FOR P = 0.01  0.01  0.99
.
LET BETA  = 0.5
TITLE BETA = ^BETA
PLOT MUTPPF(P,BETA) FOR P = 0.01  0.01  0.99
.
LET BETA  = 0.7
TITLE BETA = ^BETA
PLOT MUTPPF(P,BETA) FOR P = 0.01  0.01  0.99
.
LET BETA  = 1
TITLE BETA = ^BETA
PLOT MUTPPF(P,BETA) FOR P = 0.01  0.01  0.99
.
END OF MULTIPLOT
.
JUSTIFICATION CENTER
MOVE 50 97
TEXT Muth Percent Point Functions