

|
NORMXPDFName:
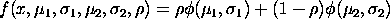
where
<SUBSET/EXCEPT/FOR qualification> where <y1> is a number, parameter, or variable; <u1> is a number, parameter, or variable; <sd1> is a number, parameter, or variable; <u2> is a number, parameter, or variable; <sd2> is a number, parameter, or variable; <pmix> is a number, parameter, or variable in the range 0 to 1; <y2> is a variable or a parameter (depending on what <y1> is) where the computed normal mixture pdf value is stored; and where the <SUBSET/EXCEPT/FOR qualification> is optional.
LET A = NORMXPDF(3,U1,SD1,U2,SD2,P) LET Y = NORMXPDF(X,U1,SD1,U2,SD2,P)
LET SD1 = <value> LET U2 = <value> LET SD2 = <value> LET P = <value> NORMAL MIXTURE PROBABILITY PLOT Y You can generate random numbers from a normal mixture distribution as follows:
LET SD1 = <value> LET U2 = <value> LET SD2 = <value> LET P = <value> LET Y = NORMAL MIXTURE RANDOM NUMBERS FOR I = 1 1 1000
MULTIPLOT CORNER COORDINATES 5 5 95 95 LET U1 = 0 LET SD1 = 1 LET U2 = 5 LET SD2 = 3 TITLE P = 0.2 PLOT NORMXPDF(X,U1,SD1,U2,SD2,0.2) FOR X = -5 0.1 15 TITLE P = 0.4 PLOT NORMXPDF(X,U1,SD1,U2,SD2,0.4) FOR X = -5 0.1 15 TITLE P = 0.6 PLOT NORMXPDF(X,U1,SD1,U2,SD2,0.6) FOR X = -5 0.1 15 TITLE P = 0.8 PLOT NORMXPDF(X,U1,SD1,U2,SD2,0.8) FOR X = -5 0.1 15 END OF MULTIPLOT
Date created: 6/5/2001 |