NORMXPPF

NORMXPPF (LET)

Library Function

Compute the percent point function of a mixture of two normal distributions.

The normal mixture distribution has the following cumulative distribution function:

where is a normal probability density function with mean and standard deviation , is a real number between 0 and 1 that defines the mixing proportions, and x is a real number.

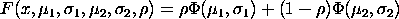
The percent point function is the inverse of the cumulative distribution function. That is, given a probability value, it returns the corresponding x value. The percent point function for the mixture of two normal distributions is computed numerically.

LET <y2> = NORMXPPF(<p>,<u1>,<sd1>, <u2>,<sd2>,<pmix>)
                        <SUBSET/EXCEPT/FOR qualification>
where <p> is a number, parameter, or variable containing probability values between 0 and 1;
<u1> is a number, parameter, or variable;
            <sd1> is a number, parameter, or variable;
            <u2> is a number, parameter, or variable;
            <sd2> is a number, parameter, or variable;
            <pmix> is a number, parameter, or variable in the range 0 to 1;
            <y2> is a variable or a parameter (depending on what <p> is) where the computed normal mixture ppf value is stored;
and where the <SUBSET/EXCEPT/FOR qualification> is optional.

LET A = NORMXPPF(0.95,0,1,10,20,0.2)
LET A = NORMXPPF(0.90,U1,SD1,U2,SD2,P)
LET Y = NORMXPPF(P,U1,SD1,U2,SD2,PMIX)

You can generate a probability plot for a normal mixture distribution as follows:
LET U1 = <value>
LET SD1 = <value>
LET U2 = <value>
LET SD2 = <value>
LET P = <value>
NORMAL MIXTURE PROBABILITY PLOT Y


You can generate random numbers from a normal mixture distribution as follows:

LET U1 = <value>
LET SD1 = <value>
LET U2 = <value>
LET SD2 = <value>
LET P = <value>
LET Y = NORMAL MIXTURE RANDOM NUMBERS FOR I = 1 1 1000

None

None

NORMXPDF = Compute the normal mixture probability density function.
NORMXCDF	= Compute the normal mixture cumulative distribution function.
NORCDF	= Compute the normal cumulative distribution function.
NORPDF	= Compute the normal probability density function.
NORPPF	= Compute the normal percent point function.

"Continuous Univariate Distributions: Volume 1", Johnson, Kotz, and Balakrishnan, John Wiley and Sons, 1994.

Distributional Modeling

1998/5

MULTIPLOT 2 2
MULTIPLOT CORNER COORDINATES 5 5 95 95
YLIMITS -5 15
XLIMITS 0 1
MAJOR XTIC MARK NUMBER 6
MINOR XTIC MARK NUMBER 1
LET U1 = 0
LET SD1 = 1
LET U2 = 5
LET SD2 = 3
TITLE P = 0.2
PLOT NORMXPPF(P,U1,SD1,U2,SD2,0.2) FOR P = 0.01 0.01 0.99
TITLE P = 0.4
PLOT NORMXPPF(P,U1,SD1,U2,SD2,0.4) FOR P = 0.01 0.01 0.99
TITLE P = 0.6
PLOT NORMXPPF(P,U1,SD1,U2,SD2,0.6) FOR P = 0.01 0.01 0.99
TITLE P = 0.8
PLOT NORMXPPF(P,U1,SD1,U2,SD2,0.8) FOR P = 0.01 0.01 0.99
END OF MULTIPLOT