PARPPF

PARPPF (LET)

Library Function

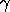Compute the Pareto percent point function with shape parameters and a.

The standard form of the Pareto percent point function is:

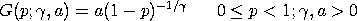
with and a denoting the tail length shape parameter and the lower bound parameter, respectively. The default value of a is 1.

Note that although the a parameter is typically called a location parameter (and it is in the sense that it defines the lower bound), it is not a location parameter in the technical sense that the following relation does not hold:

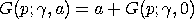
For this reason, Dataplot treats a as a shape parameter. In Dataplot, the a shape parameter is optional with a default value of 1.

LET <y> = PARPPF(<p>,<gamma>,<a>,<loc>,<scale>)
                        <SUBSET/EXCEPT/FOR qualification>
where <p> is a variable, a number, or a parameter in the interval (0,1);
            <gamma> is a number or parameter that specifies the tail length shape parameter;
            <a> is a number or parameter that specifies the optional lower bound shape parameter;
            <loc> is a number or parameter that specifies the optional location parameter;
            <scale> is a number or parameter that specifies the optional scale parameter;
            <y> is a variable or a parameter (depending on what <p> is) where the computed Pareto ppf value is saved;
and where the <SUBSET/EXCEPT/FOR qualification> is optional.

The a, loc, and scale parameters are all optional.

LET A = PARPPF(0.95,1.5)
LET A = PARPPF(0.95,1.5,2)
LET Y = PARPPF(P,GAMMA,A,LOC,SCALE)
PLOT PARPPF(P,GAMMA,A,LOC,SCALE) FOR P = 0 0.01 0.99

The Pareto percent point function can be extended with location and scale parameters by using the relationship

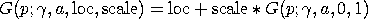
Most applications of the Pareto distribution use the standard form (location = zero, scale = one).

None

None

PARCDF	= Compute the Pareto cumulative distribution function.
PARCHAZ	= Compute the Pareto cumulative hazard function.
PARHAZ	= Compute the Pareto hazard function.
PARPDF	= Compute the Pareto probability density function.
GEPPDF	= Compute the generalized Pareto probability density function.
EV1PDF	= Compute the extreme value type I probability density function.
WEIPDF	= Compute the Weibull probability density function.
EXPPDF	= Compute the exponential probability density function.

"Continuous Univariate Distributions: Volume 1", Second Edition, Johnson, Kotz, and Balakrishnan, Wiley, 1994, chapter 19.

Distributional Modeling

1994/4

 
MULTIPLOT 2 2
MULTIPLOT CORNER COORDINATES 0 0 100 95
MULTIPLOT SCALE FACTOR 2
.
CASE ASIS
TITLE CASE ASIS
LABEL CASE ASIS
TITLE DISPLACEMENT 2
Y1LABEL DISPLACEMENT 15
X1LABEL DISPLACEMENT 12
X1LABEL Probability
Y1LABEL X
.
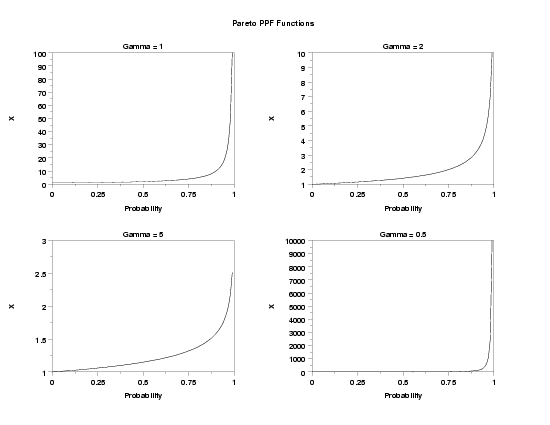
TITLE Gamma = 1
PLOT PARPPF(P,1) FOR P = 0  0.01  0.99
TITLE Gamma = 2
PLOT PARPPF(P,2) FOR P = 0  0.01  0.99
TITLE Gamma = 5
PLOT PARPPF(P,5) FOR P = 0  0.01  0.99
TITLE Gamma = 0.5
PLOT PARPPF(P,0.5) FOR P = 0  0.01  0.99
END OF MULTIPLOT
MOVE 50 97
JUSTIFICATION CENTER
TEXT Pareto PPF Functions