POOLED VARIANCE-COVARIANCE MATRIX

POOLED VARIANCE-COVARIANCE MATRIX (LET)

Let Subcommand

Compute the pooled variance-covariance matrix of a matrix.

This command operates on a matrix (M) and a group id variable (TAG). The TAG variable has the same number of rows as the matrix M. The values of TAG are typically integers that identify the group to which the corresponding row of the matrix belongs.

The POOLED VARIANCE-COVARIANCE MATRIX command returns a matrix that contains a pooled variance-covariance matrix, which is defined as:

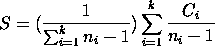
where n_i is the number of elements in group i and C_i is the variance-covariance matrix of the rows belonging to group i.

LET <mat2> = POOLED VARIANCE-COVARIANCE MATRIX <mat1> <tag>
where <mat1> is a matrix for which the pooled covariance matrix is to be computed;
              <tag> is the group-id variable;
and where <mat2> is a matrix where the resulting pooled covariance matrix is saved.

LET <mat3> = POOLED VARIANCE-COVARIANCE MATRIX <mat1> <mat2>
where <mat1> is a matrix containing the data for group 1;
              <mat2> is a matrix containing the data for group 2;
and where <mat3> is a matrix where the resulting pooled variance-covariance matrix is saved.

This syntax can be used for the case where there are exactly two groups. In this case, the data for each group is stored in a separate matrix and no group id variable is required.

LET COV = POOLED VARIANCE-COVARIANCE MATRIX M TAG

Matrices are created with either the READ MATRIX command or the MATRIX DEFINITION command. Enter HELP MATRIX DEFINITION and HELP READ MATRIX for details.

None

None

VARIANCE-COVARIANCE MATRIX	= Compute the variance-covariance matrix of a matrix.
CORRELATION MATRIX	= Compute the correlation matrix of a matrix.
MATRIX GROUP SD	= Compute the group means for a matrix.
MATRIX GROUP SD	= Compute the group standard deviations for a matrix.

"Applied Multivariate Statistical Analysis", Third Edition, Johnson and Wichern, Prentice-Hall, 1992.

Multivariate Analysis

1998/8

DIMENSION 50 COLUMNS
SKIP 25
READ IRIS.DAT Y1 Y2 Y3 Y4 TAG
LET N = SIZE Y1
LET M = MATRIX DEFINITION Y1 N 4
LET Z = POOLED VARIANCE-COVARIANCE MATRIX M TAG

. Perform a Fisher's dsicriminant analysis on Iris data.
.
. READ DATA, 3 GROUPS (N1=N2=N3=3), 2 VARIABLES
FEEDBACK OFF
DIMENSION 200 COLUMNS
SKIP 25
READ IRIS.DAT SEPLENG SEPWIDTH PETLENG PETWIDTH TAG
KIP 0
LET NTOT = SIZE SEPLENG
LET X = MATRIX DEFINITION SEPLENG NTOT 4
LET P = MATRIX NUMBER OF COLUMNS X
.
LET GROUPID = DISTINCT TAG
LET NG = SIZE GROUPID
LET XMGRAND = MATRIX COLUMN MEANS X
.
. CALCULATE B0 = SUM (I=1,NG) (XBARi - XBARALL)(XBARi-XBARALL)'
.
LET DIAG = 0 FOR I = 1 1 P
LET B0 = DIAGONAL MATRIX DIAG
.
LOOP FOR K = 1 1 NG
        LET N^K = SIZE TAG SUBSET TAG = K
        LET XMEANI = MATRIX COLUMN MEANS X SUBSET TAG = K
        LET XMEANI= XMEANI - XMGRAND
        LET B0TEMP = VECTOR TIMES TRANSPOSE XMEANI
        LET B0 = MATRIX ADDITION B0 B0TEMP
END OF LOOP
.
. CALCULATE Spooled = (N1-1)S1 + .. + (Ng-1)Sg)/(N1+ .. + Ng - g)
LET SPOOL = POOLED VARIANCE-COVARIANCE MATRIX X TAG
LET DENOM = NTOT - NG
LET WINVB = MATRIX MULTIPLICATION SPOOL DENOM
LET WINVB = MATRIX INVERSE WINVB
LET WINVB = MATRIX MULTIPLICATION WINVB B0
.
. COMPUTE EIGENVALUES AND SORT IN DECREASING ORDER
. COMPUTE EIGENVECTORS, ONLY KEEP REAL COMPONENT, SORT
.
LET E = MATRIX EIGENVALUES WINVB
LET EV = MATRIX EIGENVECTORS WINVB
LET INDX = SEQUENCE 1 1 P
RETAIN E FOR I = 1 1 P
LET ESORT = SORTC E INDX
LET REVERSE = SEQUENCE P 1 1
LET REVERSE = SORTC REVERSE ESORT INDX
LET EVECT = DIAGONAL MATRIX DIAG
. NORMALIZE L'SpooledL =1
. DIST = L'SpooledL, MULTIPLY EIGENVECTOR BY 1/SQRT(DIST)
LOOP FOR K = 1 1 P
        LET LTAG = INDX(K)
        RETAIN EV^K FOR I = 1 1 P
        LET EVECT^LTAG = EV^K
        LET DIST = QUADRATIC FORM SPOOL EVECT^LTAG
        LET EVECT^LTAG = (1/SQRT(DIST))*EVECT^LTAG
END OF LOOP
. PLOT FIRST 2 DISCRIMINANTS
LET ZY = LINEAR COMBINATION X EVECT1
LET ZX = LINEAR COMBINATION X EVECT2
DEVICE 1 OFF
MEAN PLOT ZY TAG
LET GMEANY = YPLOT
MEAN PLOT ZX TAG
LET GMEANX = YPLOT
RETAIN GMEANX GMEANY SUBSET TAGPLOT = 1
DEVICE 1 ON
Y1LABEL FIRST DISCRIMINANT
X1LABEL SECOND DISCRIMINANT
CHARACTER CIRCLE SQUARE TRIANGLE
LINE BLANK ALL
LEGEND 1 CIRC() - SPECIES 1
LEGEND 2 SQUA() - SPECIES 2
LEGEND 3 TRIA() - SPECIES 3
LEGEND FONT DUPLEX
LEGEND SIZE 1.2
TITLE PLOT FIRST 2 DISCRIMINANT FUNCTIONS
PLOT ZY ZX TAG
PRINT "FISHER's DISCRIMINANT ANALYSIS"
PRINT " "
PRINT " "
PRINT "B0 MATRIX (= between group sums of cross-products):"
PRINT B0
PRINT " "
PRINT " "
PRINT "POOLED VARIANCE-COVARIANCE MATRIX:"
PRINT SPOOL
PRINT " "
PRINT " "
PRINT "EIGENVALUES:"
PRINT ESORT
PRINT " "
PRINT " "
PRINT "COLUMNS ARE THE DISCRIMINANT FUNCTIONS:"
PRINT EVECT
PRINT " "
PRINT " "
PRINT "GROUP MEANS:"
PRINT GMEANX GMEANY




 FISHER's DISCRIMINANT ANALYSIS
  
  
 B0 MATRIX (= between group sums of cross-products):

 VARIABLES--B01            B02            B03            B04     

   0.1264242E+01 -0.3990533E+00  0.4142301E+01  0.1332920E+01
  -0.3990533E+00  0.2268987E+00 -0.1515458E+01 -0.1713200E+00
   0.4142301E+01 -0.1515458E+01  0.1400072E+02  0.3853480E+01
   0.1332920E+01 -0.1713200E+00  0.3853480E+01  0.2021600E+01
  
  
 POOLED VARIANCE-COVARIANCE MATRIX:

 VARIABLES--SPOOL1         SPOOL2         SPOOL3         SPOOL4  

   0.2650082E+00  0.9272107E-01  0.1675143E+00  0.3840136E-01
   0.9272107E-01  0.1153878E+00  0.5524353E-01  0.3271021E-01
   0.1675143E+00  0.5524353E-01  0.1851877E+00  0.4266530E-01
   0.3840136E-01  0.3271021E-01  0.4266530E-01  0.4188163E-01
  
  
 EIGENVALUES:

 VARIABLES--ESORT   

   0.8901299E+00
   0.2225433E+00
  -0.3733565E-08
  -0.2227863E-07
  
  
 COLUMNS ARE THE DISCRIMINANT FUNCTIONS:

 VARIABLES--EVECT1         EVECT2         EVECT3         EVECT4  

  -0.1369850E+01  0.8875500E+00 -0.2325767E+01 -0.2739004E+01
  -0.9835795E+00 -0.9720628E+00  0.8406132E-02  0.2782870E+01
   0.3014445E+01 -0.2081234E+01  0.5611728E+00  0.1156235E+01
   0.1221005E+01  0.5894731E+01  0.4644992E+00 -0.1621946E+00
  
  
 GROUP MEANS:

 VARIABLES--GMEANX         GMEANY  

   0.1599418E+01 -0.8536139E+01
  -0.4368491E+01  0.2383637E+01
   0.3343979E+01  0.7260216E+01