POSITIVE PREDICTIVE VALUE

POSITIVE PREDICTIVE VALUE (LET)

Let Subcommand

Compute the positive predictive value between two binary variables.

Given two variables with n parired observations where each variable has exactly two possible outcomes, we can generate the following 2x2 table:

	Variable 2
Variable 1	Success	Failure	Row Total
Success	N11	N12	N11 + N12
Failure	N21	N22	N21 + N22
Column Total	N11 + N21	N12 + N22	N

The parameters N₁₁, N₁₂, N₂₁, and N₂₂ denote the counts for each category.

Success and failure can denote any binary response. Dataplot expects "success" to be coded as "1" and "failure" to be coded as "0". Some typical examples would be:

1. Variable 1 denotes whether or not a patient has a disease (1 denotes disease is present, 0 denotes disease not present). Variable 2 denotes the result of a test to detect the disease (1 denotes a positive result and 0 denotes a negative result).

2. Variable 1 denotes whether an object is present or not (1 denotes present, 0 denotes absent). Variable 2 denotes a detection device (1 denotes object detected and 0 denotes object not detected).

In these examples, the "ground truth" is typically given as variable 1 while some estimator of the ground truth is given as variable 2.

The positive predictive value is then N₁₁/(N₁₁+N₂₁). This is the conditional probability of variable 1 being true given that variable 2 is true. In the context of the first example above, this is the probability that the disease is present when there is a positive test result.

Fleiss and his co-authors recommend positive predictive value and negative predictive value as an alternative to false positive and false negative due to the fact that the definitions of false positive and false negative have been inconsistent in the literature.

LET <par> = POSITIVE PREDICTIVE VALUE <y1> <y2>
                        <SUBSET/EXCEPT/FOR qualification>
where <y1> is the first response variable;
            <y2> is the second response variable;
            <par> is a parameter where the computed positive predictive value is stored;
and where the <SUBSET/EXCEPT/FOR qualification> is optional.

LET A = POSITIVE PREDICTIVE VALUE Y1 Y2
LET A = POSITIVE PREDICTIVE VALUE Y1 Y2 SUBSET TAG > 2

The two variables must have the same number of elements.

There are two ways you can define the response variables:
1. Raw data - in this case, the variables contain 0's and 1's.

   If the data is not coded as 0's and 1's, Dataplot will check for the number of distinct values. If there are two distinct values, the minimum value is converted to 0's and the maximum value is converted to 1's. If there is a single distinct value, it is converted to 0's if it is less than 0.5 and to 1's if it is greater than or equal to 0.5. If there are more than two distinct values, an error is returned.

2. Summary data - if there are two observations, the data is assummed to be the 2x2 summary table. That is,
   Y1(1) = N11
   Y1(2) = N21
   Y2(1) = N12
   Y2(2) = N22
   

The following additional commands are supported
TABULATE FALSE POSITIVE Y1 Y2 X
CROSS TABULATE FALSE POSITIVE Y1 Y2 X1 X2

POSITIVE PREDICTIVE VALUE PLOT Y1 Y2 X
CROSS TABULATE POSITIVE PREDICTIVE VALUE PLOT Y1 Y2 X1 X2

BOOTSTRAP POSITIVE PREDICTIVE VALUE PLOT Y1 Y2
JACKNIFE POSITIVE PREDICTIVE VALUE PLOT Y1 Y2

None

None

NEGATIVE PREDICTIVE VALUE	= Compute the negative predictive value between two binary variables.
TRUE POSITIVES	= Compute the proportion of true positives.
TRUE NEGATIVES	= Compute the proportion of true negatives.
FALSE POSITIVES	= Compute the proportion of false negatives.
FALSE NEGATIVES	= Compute the proportion of false negatives.
TEST SENSITIVITY	= Compute the test sensitivity.
TEST SPECIFICITY	= Compute the test specificity.
ODDS RATIO	= Compute the bias corrected log(odds ratio).
ODDS RATIO STANDARD ERROR	= Compute the standard error of the bias corrected log(odds ratio).
RELATIVE RISK	= Compute the relative risk.
TABULATE	= Compute a statistic for data with a single grouping variable.
CROSS TABULATE	= Compute a statistic for data with two grouping variables.
STATISTIC PLOT	= Generate a plot of a statistic for data with a single grouping variable.
CROSS TABULATE PLOT	= Generate a plot of a statistic for data with two grouping variables.
BOOTSTRAP PLOT	= Generate a bootstrap plot for a given statistic.

Fleiss, Levin, and Paik (2003), "Statistical Methods for Rates and Proportions", Third Edition, Wiley, chapter 1.

Categorical Data Analysis

2007/4

 
let n = 1
.
let p = 0.2
let y1 = binomial rand numb for i = 1 1 100
let p = 0.1
let y2 = binomial rand numb for i = 1 1 100
.
let p = 0.4
let y1 = binomial rand numb for i = 101 1 200
let p = 0.08
let y2 = binomial rand numb for i = 101 1 200
.
let p = 0.15
let y1 = binomial rand numb for i = 201 1 300
let p = 0.18
let y2 = binomial rand numb for i = 201 1 300
.
let p = 0.6
let y1 = binomial rand numb for i = 301 1 400
let p = 0.45
let y2 = binomial rand numb for i = 301 1 400
.
let p = 0.3
let y1 = binomial rand numb for i = 401 1 500
let p = 0.1
let y2 = binomial rand numb for i = 401 1 500
.
let x = sequence 1 100 1 5
.
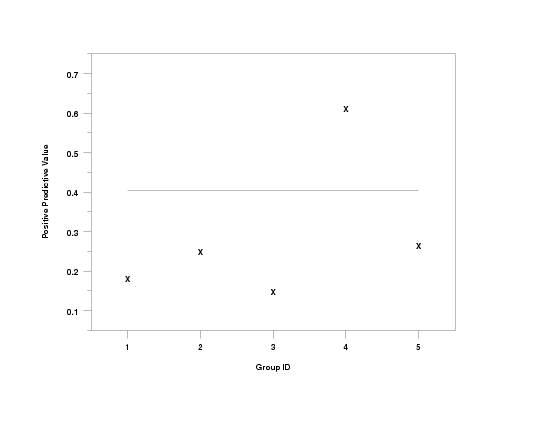
let a = positive predictive value y1 y2 subset x = 1
tabulate positive predictive value y1 y2 x
.
label case asis
xlimits 1 5
major xtic mark number 5
minor xtic mark number 0
xtic mark offset 0.5 0.5
ytic mark offset 0.05 0.05
y1label Positive Predictive Value
x1label Group ID
character x blank
line blank solid
.
positive predictive value plot y1 y2 x