RGTPPF

RGTPPF (LET)

Library Function

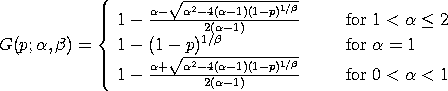
Compute the reflected generalized Topp and Leone percent point function with shape parameters alpha and beta.

The standard reflected generalized Topp and Leone distribution has the following percent point function:

with and denoting the shape parameters.

The standard distribution can be generalized with lower and upper bound parameters, a and b, respectively, by utilizing the following relation:

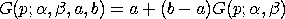
The lower and upper limits are related to the location and scale parameters as follows:

location = a
scale = b - a

LET <y> = RGTPDF(<p>,<alpha>,<beta>,<a>,<b>)
                        <SUBSET/EXCEPT/FOR qualification>
where <p> is a number, parameter, or variable containing values in the interval (0,1);
            <y> is a variable or a parameter (depending on what <p> is) where the computed reflected generalized Topp and Leone ppf value is stored;
            <alpha> is a number, parameter, or variable in the interval (0, 2) that specifies the first shape parameter;
            <beta> is a positive number, parameter, or variable that specifies the second shape parameter;
            <a> is a number, parameter, or variable that specifies the lower limit;
            <b> is a number, parameter, or variable that specifies the upper limit;
and where the <SUBSET/EXCEPT/FOR qualification> is optional.

If <a> and <b> are omitted, they default to 0 and 1, respectively.

LET A = RGTPPF(0.95,0.2,1.2)
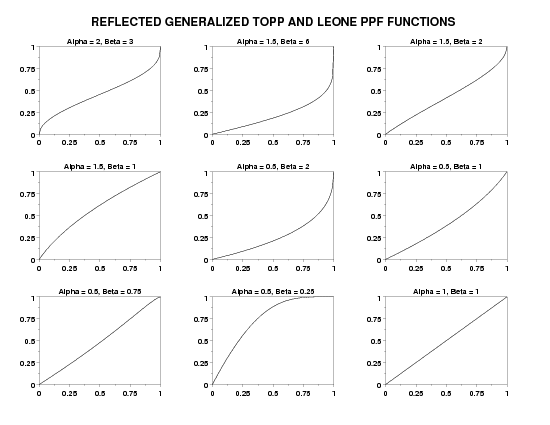
LET Y = RGTPPF(P,0.5,2)
PLOT RGTPPF(P,2,3) FOR P = 0 0.01 1

None

None

RGTCDF	= Compute the reflected generalized Topp and Leone cumulative distribution function.
RGTPDF	= Compute the reflected generalized Topp and Leone probability density function.
GTLPDF	= Compute the generalized Topp and Leone probability density function.
TOPPDF	= Compute the Topp and Leone probability density function.
TSPPDF	= Compute the two-sided power probability density function.
BETPDF	= Compute the beta probability density function.
TRIPDF	= Compute the triangular probability density function.
TRAPDF	= Compute the trapezoid probability density function.
UNIPDF	= Compute the uniform probability density function.
POWPDF	= Compute the power probability density function.
JSBPDF	JSBPDF = Compute the Johnson SB probability density function.

Samuel Kotz and J. Rene Van Dorp 2004, "Beyond Beta: Other Continuous Families of Distributions with Bounded Support and Applications", World Scientific, chapter 7.

Distributional Modeling

2007/2

 
LABEL CASE ASIS
TITLE CASE ASIS
TITLE OFFSET 2
.
MULTIPLOT 3 3
MULTIPLOT CORNER COORDINATES 0 0 100 95
MULTIPLOT SCALE FACTOR 3
.
LET ALPHA = 2
LET BETA  = 3
TITLE Alpha = ^alpha, Beta = ^beta
PLOT RGTPPF(P,ALPHA,BETA) FOR P = 0  0.01  1
.
LET ALPHA = 1.5
LET BETA  = 6
TITLE Alpha = ^alpha, Beta = ^beta
PLOT RGTPPF(P,ALPHA,BETA) FOR P = 0  0.01  1
.
LET ALPHA = 1.5
LET BETA  = 2
TITLE Alpha = ^alpha, Beta = ^beta
PLOT RGTPPF(P,ALPHA,BETA) FOR P = 0  0.01  1
.
LET ALPHA = 1.5
LET BETA  = 1
TITLE Alpha = ^alpha, Beta = ^beta
PLOT RGTPPF(P,ALPHA,BETA) FOR P = 0  0.01  1
.
LET ALPHA = 0.5
LET BETA  = 2
TITLE Alpha = ^alpha, Beta = ^beta
PLOT RGTPPF(P,ALPHA,BETA) FOR P = 0  0.01  1
.
LET ALPHA = 0.5
LET BETA  = 1
TITLE Alpha = ^alpha, Beta = ^beta
PLOT RGTPPF(P,ALPHA,BETA) FOR P = 0  0.01  1
.
LET ALPHA = 0.5
LET BETA  = 0.75
TITLE Alpha = ^alpha, Beta = ^beta
PLOT RGTPPF(P,ALPHA,BETA) FOR P = 0  0.01  1
.
LET ALPHA = 0.5
LET BETA  = 0.25
TITLE Alpha = ^alpha, Beta = ^beta
PLOT RGTPPF(P,ALPHA,BETA) FOR P = 0  0.01  1
.
LET ALPHA = 1
LET BETA  = 1
TITLE Alpha = ^alpha, Beta = ^beta
PLOT RGTPPF(P,ALPHA,BETA) FOR P = 0  0.01  1
.
END OF MULTIPLOT
.
JUSTIFICATION CENTER
MOVE 50 97
TEXT Reflected Generalized Topp and Leone PPF Functions