RIGPDF

RIGPDF (LET)

Library Function

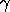Compute the reciprocal inverse Gaussian probability density function with shape parameters and .

The reciprocal inverse Gaussian distribution is the distribution of (1/X) when X has an inverse Gaussian distribution. It has the following probability density function:

with and denoting the shape parameters.

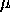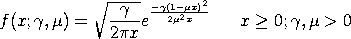
The reciprocal inverse Gaussian distribution can be computed in terms of the inverse Gaussian distribution by

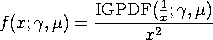
with IGPDF denoting the probability density function of the inverse Gaussian distribution. Dataplot uses this relationship to compute the probability density function.

The reciprocal inverse Gaussian distribution has mean and standard deviation .

The reciprocal inverse Gaussian distribution can be generalized with location and scale parameters in the usual way.

LET <y> = RIGPDF(<x>,<gamma>,<mu>,<loc>,<scale>)
                        <SUBSET/EXCEPT/FOR qualification>
where <x> is a variable or a parameter;
            <gamma> is number or parameter that specifies the first shape parameter;
            <mu> is number or parameter that specifies the second shape parameter;
            <loc> is number or parameter that specifies the location parameter;
            <scale> is number or parameter that specifies the scale parameter;
            <y> is a variable or a parameter (depending on what <x> is) where the computed reciprocal inverse Gaussian pdf value is stored;
and where the <SUBSET/EXCEPT/FOR qualification> is optional.

Note that the location and scale parameters are optional.

LET A = RIGPDF(3,2,1)
LET A = RIGPDF(A1,2,1)
LET X2 = RIGPDF(X1,2,3)
PLOT RIGPDF(X,2,1.5) FOR X = 0.1 0.1 5

Random numbers, probability plots, and Kolmogorov-Smirnov and chi-square goodness of fit tests can be generated with the commands:
LET GAMMA = <value>
LET MU = <value>
LET Y = RECIPROCAL INVERSE GAUSSIAN RANDOM NUMBERS ...

FOR I = 1 1 N

RECIPROCAL INVERSE GAUSSIAN PROBABILITY PLOT Y
RECIPROCAL INVERSE GAUSSIAN KOLMOGOROV-SMIRNOV ...

GOODNESS OF FIT Y

RECIPROCAL INVERSE GAUSSIAN CHI-SQUARE FIT Y


The following commands can be used to generate estimates for the shape parameters of the reciprocal inverse Gaussian distribution:

LET GAMMA1 = <value>
LET GAMMA2 = <value>
LET MU1 = <value>
LET MU2 = <value>
RECIPROCAL INVERSE GAUSSIAN PPCC PLOT Y
RECIPROCAL INVERSE GAUSSIAN KS PLOT Y


The default values for GAMMA1 and GAMMA2 are 0.5 and 25. The default values for MU1 and MU2 are 0.5 and 25.

None

None

RIGCDF	= Compute the reciprocal inverse Gaussian cumulative distribution function.
RIGCHAZ	= Compute the reciprocal inverse Gaussian cumulative hazard function.
RIGHAZ	= Compute the reciprocal inverse Gaussian hazard function.
RIGPDF	= Compute the reciprocal inverse Gaussian probability density function.
RIGPPF	= Compute the reciprocal inverse Gaussian percent point function.
IGPDF	= Compute the reciprocal inverse Gaussian probability density function.
CHSPDF	= Compute the chi-square probability density function.
FPDF	= Compute the F probability density function.
NORPDF	= Compute the normal probability density function.
TPDF	= Compute the t probability density function.
WEIPDF	= Compute the Weibull probability density function.
WALPDF	= Compute the Wald probability density function.
FLPDF	= Compute the fatigue life probability density function.

"Continuous Univariate Distributions--Volume 1", Second Edition, Johnson, Kotz, and Balakrishnan, Wiley, 1994, chapter 15.

"Statistical Distributions", Third Edition, Evans, Hastings, and Peacock, Wiley, 2000, pp. 114-116.

Distributional Modeling

1990/5: Original implementation
2003/12: Modified to treat 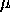as a shape parameter instead of a location parameter.

 
Y1LABEL Probability
X1LABEL X
LABEL CASE ASIS
X1LABEL DISPLACEMENT 12
Y1LABEL DISPLACEMENT 12
MULTIPLOT SCALE FACTOR 2
MULTIPLOT 2 2
MULTIPLOT CORNER COORDINATES 0 0 100 95
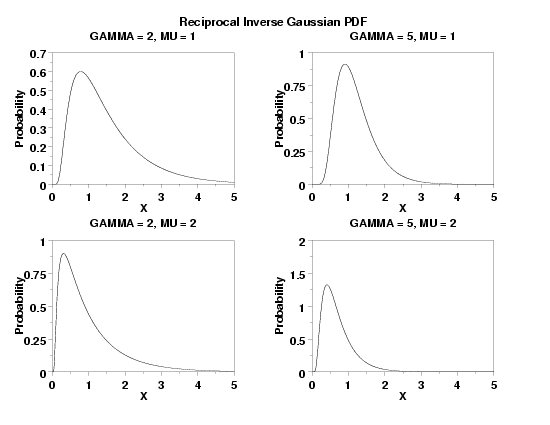
TITLE GAMMA = 2, MU = 1
PLOT RIGPDF(X,2,1) FOR X = 0.01  0.01  5
TITLE GAMMA = 5, MU = 1
PLOT RIGPDF(X,5,1) FOR X = 0.01  0.01  5
TITLE GAMMA = 2, MU = 2
PLOT RIGPDF(X,2,2) FOR X = 0.01  0.01  5
TITLE GAMMA = 5, MU = 2
PLOT RIGPDF(X,5,2) FOR X = 0.01  0.01  5
END OF MULTIPLOT
JUSTIFICATION CENTER
MOVE 50 97
CASE ASIS
TEXT Reciprocal Inverse Gaussian PDF