

|
TSOCDFName:
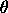
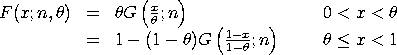
with F and G denoting the cumulative distribution functions of the two-sided ogive and the ogive distributions, respectively. This relation is given on page 230 of Kotz and Van Dorp (see Reference section below). This distribution can be extended with lower and upper bound parameters. If a and b denote the lower and upper bounds, respectively, then the location and scale parameters are:
scale = b - a The general form of the distribution can then be found by using the relation
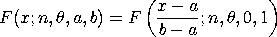
Kotz and Van Dorp note that the two-sided ogive distribution
is smooth at the reflection point (x =
<SUBSET/EXCEPT/FOR qualification> where <x> is a number, parameter, or variable containing values in the interval (a,b); <y> is a variable or a parameter (depending on what <x> is) where the computed two-sided ogive cdf value is stored; <n> is a number, parameter, or variable in the interval (≥ 0.5) that specifies the first shape parameter; <theta> is a number, parameter, or variable in the interval (a,b) that specifies the second shape parameter; <a> is a number, parameter, or variable that specifies the lower bound; <b> is a number, parameter, or variable that specifies the upper bound; and where the <SUBSET/EXCEPT/FOR qualification> is optional. If <a> and <b> are omitted, they default to 0 and 1, respectively.
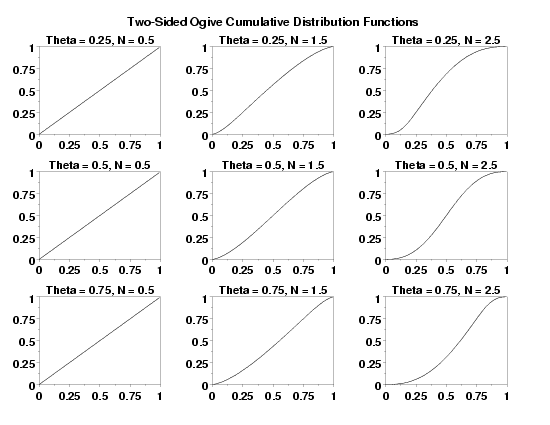
LET Y = TSOCDF(X,1.5,2.2,0,5) PLOT TSOCDF(X,1.5,2.2,0,5) FOR X = 0 0.01 5
MULTIPLOT 3 3
MULTIPLOT CORNER COORDINATES 0 0 100 95
MULTIPLOT SCALE FACTOR 3
TITLE OFFSET 2
TITLE CASE ASIS
LABEL CASE ASIS
CASE ASIS
.
LET THETAV = DATA 0.25 0.50 0.75
LET NV = DATA 0.5 1.5 2.5
.
LOOP FOR K = 1 1 3
LET THETA = THETAV(K)
LOOP FOR L = 1 1 3
LET N = NV(L)
TITLE Theta = ^THETA, N = ^N
PLOT TSOCDF(X,N,THETA) FOR X = 0 0.01 0.99
END OF LOOP
END OF LOOP
.
END OF MULTIPLOT
MOVE 50 97
JUSTIFICATION CENTER
TEXT Two-Sided Ogive Cumulative Distribution Functions
Date created: 12/13/2007 |