WISHART RANDOM NUMBER

WISHART RANDOM NUMBER GENERATOR

Let Subcommand

Generate the sample variance-covariance matrix from a random sample of size n that is distributed as a p-variate normal N_p (, ).

The Wishart distribution is a k-dimensional generalization of the chi-square distribution. The chi-square distribution is the sum of squared normal variates. The Wishart distribution is the sum of squared multivariate normal variates. The Wishart distribution has applications in Bayesian analysis.

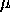In order to generate the Wishart variates, you need to specify the following:

1. - the pxp variance-covariance matrix of the multivariate normal distribution

2. - the vector of length p that defines the location parameters of the multivariate normal distribution

3. n - the sample size

What is returned is a pxp sample variance-covariance matrix.

LET <mat> = WISHART RANDOM NUMBERS <mu> <sigma> <n>
where <mu> is a variable containing the desired location parameters;
            <sigma> is a matrix containing the desired variance-covariance matrix;
            <n> is a number or parameter specifying the sample size;
and where <mat> is a matrix where the resulting Wishart random numbers are stored.

The number of rows in <mu> must equal the number of rows and columns in the <Sigma> matrix. The <Sigma> matrix must be a valid variance-covariance matrix (i.e., symmetric and positive definite).

LET MU = -5 0 5
READ MATRIX SIGMA
1 0.5 0.5
0.5 1 0.5
0.5 0.5 1
END OF DATA
LET N = 500
LET M = WISHART RANDOM NUMBERS MU SIGMA N

Dataplot generates the Wishart matrix using algorithm AS 53 (routine WSHRT) from the Applied Statistics journal. See the Reference below for details.

As with univariate random numbers, the Wishart random numbers are built on an underlying uniform random number generator. Dataplot supports a number of different uniform random number generators. For details, enter
HELP SET RANDOM NUMBER GENERATOR

None

None

RANDOM NUMBERS	= Generate random numbers for 90+ univariate distributions.
SET RANDOM NUMBER GENERATOR	= Specify which univariate generator to use.
MULTIVARIATE NORM RAND NUMB	= Generate multivariate normal random numbers.
MULTIVARIATE T RANDOM NUMBERS	= Generate multivariate t random numbers.
INDEPENDENT UNIFORM RAND NUMB	= Generate random numbers for independent uniform distributions.
MULTINOMIAL RANDOM NUMBERS	= Generate random numbers for a multinomial distribution.
DIRICHLET RANDOM NUMBERS	= Generate random numbers for a Dirichlet distribution.

"Algorithm AS 53: Wishart Variate Generator", Smith and Hocking, Applied Statistics, 1972, Vol. 21, No. 3.

"Statistical Distributions", Third Edition, Evans, Hastings, and Peacock, Wiley, 2000, pp. 204-205.

Bayesian Analysis

2003/3

 
dimension 100 columns
.
.  Test Wishart random numbers
.
read matrix sigma
 1.0        -0.707107  0.0  0.0 0.0
-0.707107    1.0       0.5  0.5 0.5
 0.0         0.5       1.0  0.5 0.5
 0.0         0.5       0.5  1.0 0.5
 0.0         0.5       0.5  0.5 1.0
end of data
.
let mu = data 0 0 0 0 0
let n = 200
.
let w = wishart random numbers mu sigma n
.
set write decimals 3
print w
    

The following outout is generated.

 
  
         MATRIX W       --            5 ROWS
                        --            5 COLUMNS

 VARIABLES--W1             W2             W3             W4             W5      

          0.923         -0.653         -0.024          0.577         -0.013
         -0.653          0.462          0.017         -0.408          0.009
         -0.024          0.017          0.527          0.558          0.564
          0.577         -0.408          0.558          2.045          0.644
         -0.013          0.009          0.564          0.644          1.121