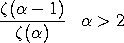ZETPDF
Name:
Type:
Purpose:
Compute the Zeta probability mass function.
Description:
The zeta distribution has the following probability mass
function:
with 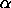 denoting the shape parameter and
denoting the shape parameter and
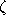 denoting
the Riemann zeta function denoting
the Riemann zeta function
Some sources parameterize this distribution with
s = 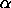 - 1 (so that the distribution is defined for s > 0).
- 1 (so that the distribution is defined for s > 0).
The zeta distribution becomes more long-tailed as the
value of 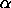 gets closer to 1.
gets closer to 1.
The mean and variance of the Zeta distribution are
The development of the zeta distribution was motivated by
Zipf's law (from the linguistics community). Zipf's law
states that the frequency of occurence of any word is
approximately inversely proportional to its rank in the
frequency table. When Zipf's law is applicable, plotting
the frequency table on a log-log scale (i.e., log(frequency)
versus log(rank order)) should show a linear pattern.
Note that Zipf's law is an empirical (as oppossed to a
theoretical) law. However, Zipf's law has served as a
useful model for many different kinds of phenomena (not just
word counts).
Syntax:
LET <y> = ZETPDF(<x>,<alpha>)
<SUBSET/EXCEPT/FOR qualification>
where <x> is a positive integer variable, number, or
parameter;
<alpha> is a number or parameter greater than 1 that
specifies the shape parameter;
<y> is a variable or a parameter where the computed
zeta pdf value is stored;
and where the <SUBSET/EXCEPT/FOR qualification> is optional.
Examples:
LET A = ZETPDF(3,1.5)
LET Y = ZETPDF(X1,2.3)
PLOT ZETPDF(X,2.3) FOR X = 1 1 50
Note:
The zeta distribution is the limiting case of the
Zipf distribution. Note that zeta
distribution and Zipf distribution tend to be used interchangeably
in the literature. The primary distinction is that the Zipf
distribution is bounded in the upper tail while the zeta
distribution is unbounded in the upper tail. When the
upper bound for the Zipf distribution is sufficiently large, the
zeta distribution is typically used as an approximation.
Note:
For a number of commands utilizing the zeta distribution,
it is convenient to bin the data. There are two basic ways
of binning the data.
- For some commands (histograms, maximum likelihood
estimation), bins with equal size widths are required.
This can be accomplished with the following commands:
LET AMIN = MINIMUM Y
LET AMAX = MAXIMUM Y
LET AMIN2 = AMIN - 0.5
LET AMAX2 = AMAX + 0.5
CLASS MINIMUM AMIN2
CLASS MAXIMUM AMAX2
CLASS WIDTH 1
LET Y2 X2 = BINNED Y
- For some commands, unequal width bins may be
helpful. In particular, for the chi-square goodness
of fit, it is typically recommended that the minimum
class frequency be at least 5. In this case, it may
be helpful to combine small frequencies in the tails.
Unequal class width bins can be created with the
commands
LET MINSIZE = <value>
LET Y3 XLOW XHIGH = INTEGER FREQUENCY TABLE Y
If you already have equal width bins data, you can
use the commands
LET MINSIZE = <value>
LET Y3 XLOW XHIGH = COMBINE FREQUENCY TABLE Y2 X2
The MINSIZE parameter defines the minimum class
frequency. The default value is 5.
Note:
You can generate Zeta random numbers and probability
plots with the following commands:
LET N = <value>
LET ALPHA = <value>
LET Y = ZETA RANDOM NUMBERS FOR I = 1 1 N
ZETA PROBABILITY PLOT Y
ZETA PROBABILITY PLOT Y2 X2
ZETA PROBABILITY PLOT Y3 XLOW XHIGH
To obtain the maximum likelihood estimate of
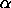 ,
enter one the commands (Y denotes raw data, Y2 denotes
frequencies, and X2 denotes the class mid-points): ,
enter one the commands (Y denotes raw data, Y2 denotes
frequencies, and X2 denotes the class mid-points):
ZETA MAXIMUM LIKELIHOOD Y
ZETA MAXIMUM LIKELIHOOD Y2 X2
The ZETA MAXIMUM LIKELIHOOD command will actually generate
the following three numerical estimates of
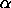 . .
- The first estimate is based on the ratio of the
frequencies of the first group (f1) and
the second group (f2). The resulting
estimate is
If either f1 or f2
is zero, this estimate is not computed. This estimate is
used as the starting value for the maximum likelihood
method.
- The method of moment estimate is computed by solving
the following equation
with  denoting the sample mean. Note that this method will not
return an estimate ≤ 2 (the mean of the zeta distribution
is only defined for
denoting the sample mean. Note that this method will not
return an estimate ≤ 2 (the mean of the zeta distribution
is only defined for
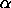 > 2).
If an error message is returned stating that method of
moment estimate is unable to find a bracketing interval,
this is an indication that the value of > 2).
If an error message is returned stating that method of
moment estimate is unable to find a bracketing interval,
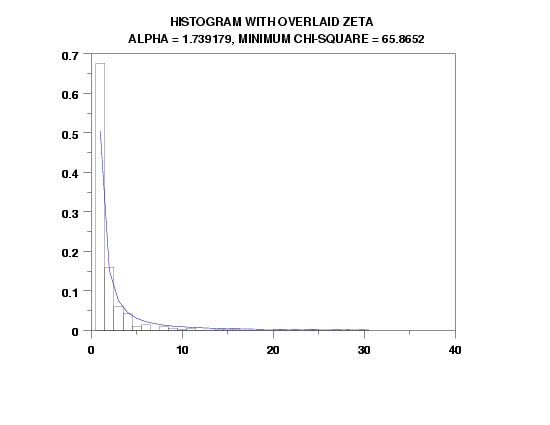
this is an indication that the value of
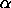 is ≤ 2.
is ≤ 2.
- The maximum likelihood estimate is computed by solving
the following equation
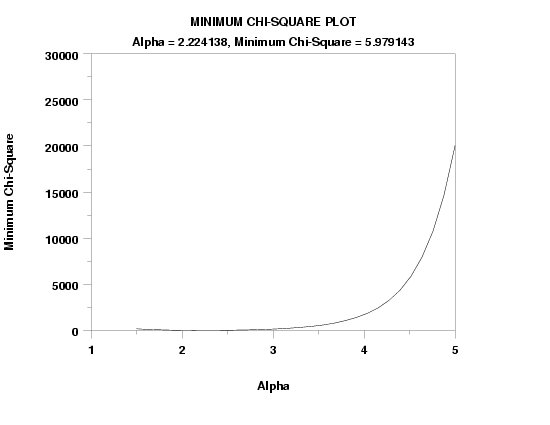
You can also generate an estimate of
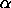 based on the maximum ppcc value or the minimum chi-square
goodness of fit with the commands
based on the maximum ppcc value or the minimum chi-square
goodness of fit with the commands
LET ALPHA1 = <value>
LET ALPHA2 = <value>
ZETA KS PLOT Y
ZETA KS PLOT Y2 X2
ZETA KS PLOT Y3 XLOW XHIGH
ZETA PPCC PLOT Y
ZETA PPCC PLOT Y2 X2
ZETA PPCC PLOT Y3 XLOW XHIGH
The default values of ALPHA1 and ALPHA2 are 1.5 and 5,
respectively. Due to the discrete nature of the percent point
function for discrete distributions, the ppcc plot will not be
smooth. For that reason, if there is sufficient sample size
the KS PLOT (i.e., the minimum chi-square value) is typically
preferred. Also, since the data is integer values, one of the
binned forms is preferred for these commands.
To generate a chi-square goodness of fit test, enter the
commands
LET ALPHA = <value>
ZETA CHI-SQUARE GOODNESS OF FIT Y2 X2
ZETA CHI-SQUARE GOODNESS OF FIT Y3 XLOW XHIGH
Default:
Synonyms:
Related Commands:
|
ZETCDF
|
= Compute the Zeta cumulative distribution function.
|
|
ZETPPF
|
= Compute the Zeta percent point function.
|
|
ZIPPDF
|
= Compute the Zipf cumulative distribution function.
|
|
YULPDF
|
= Compute the Yule probability mass function.
|
|
BGEPDF
|
= Compute the beta-geometric (Waring) probability mass
function.
|
|
BTAPDF
|
= Compute the Borel-Tanner probability mass function.
|
|
DLGPDF
|
= Compute the logarithmic series probability mass function.
|
|
INTEGER FREQUENCY TABLE
|
= Generate a frequency table at
|
|
COMBINE FREQUENCY TABLE
|
= Combine low frequency classes in a frequency table.
|
|
KS PLOT
|
= Generate a minimum chi-square plot.
|
|
MAXIMUM
LIKELIHOOD
|
= Perform maximum likelihood estimation for a
distribution.
|
Reference:
Johnson, Kotz, and Kemp (1992), "Univariate Discrete
Distributions", Second Edition, Wiley, pp. 465-471.
Devroye (1986), "Non-Uniform Random Variate Generation",
Springer-Verlang, New York.
Applications:
Implementation Date:
Program:
let alpha = 2.3
let y = zeta random numbers for i = 1 1 500
.
let y3 xlow xhigh = integer frequency table y
class lower 0.5
class width 1
let amax = maximum y
let amax2 = amax + 0.5
class upper amax2
let y2 x2 = binned y
.
zeta mle y
let alpha = alphaml
zeta chi-square goodness of fit y3 xlow xhigh
relative histogram y2 x2
limits freeze
pre-erase off
line color blue
title Histogram with Overlaid Zeta cr() ...
Alpha = ^alphaml, Minimum Chi-Square = ^statval
plot zetpdf(x,alphaml) for x = 1 1 amax
limits
pre-erase on
line color black
.
label case asis
x1label Alpha
y1label Minimum Chi-Square
title Minimum Chi-Square Plot
zeta ks plot y3 xlow xhigh
let alpha = shape
case asis
justification center
move 50 92
text Alpha = ^alpha, Minimum Chi-Square = ^minks
zeta chi-square goodness of fit y3 xlow xhigh
ZETA PARAMETER ESTIMATION:
SUMMARY STATISTICS:
NUMBER OF OBSERVATIONS = 500
SAMPLE MEAN = 1.992000
SAMPLE STANDARD DEVIATION = 2.833371
SAMPLE MINIMUM = 1.000000
SAMPLE MAXIMUM = 30.00000
SAMPLE FIRST FREQUENCY = 0.6760000
SAMPLE SECOND FREQUENCY = 0.1600000
ESTIMATION BY FIRST TWO FREQUENCIES:
ESTIMATE OF ALPHA = 2.078951
APPROXIMATE VARIANCE = 0.1379520E-01
ESTIMATION BY FIRST MOMENT:
ESTIMATE OF ALPHA = 2.481861
MAXIMUM LIKELIHOOD ESTIMATION:
ESTIMATE OF ALPHA = 1.739179
APPROXIMATE VARIANCE = 0.1392758E-02
ALPHAFR, ALPHAMOM, AND ALPHAML WILL BE SAVED AS INTERNAL PARAMETERS.
CHI-SQUARED GOODNESS-OF-FIT TEST
NULL HYPOTHESIS H0: DISTRIBUTION FITS THE DATA
ALTERNATE HYPOTHESIS HA: DISTRIBUTION DOES NOT FIT THE DATA
DISTRIBUTION: ZETA
SAMPLE:
NUMBER OF OBSERVATIONS = 500
NUMBER OF NON-EMPTY CELLS = 9
NUMBER OF PARAMETERS USED = 1
TEST:
CHI-SQUARED TEST STATISTIC = 65.86520
DEGREES OF FREEDOM = 7
CHI-SQUARED CDF VALUE = 1.000000
ALPHA LEVEL CUTOFF CONCLUSION
10% 12.01704 REJECT H0
5% 14.06714 REJECT H0
1% 18.47531 REJECT H0
CELL NUMBER, LOWER BIN POINT, UPPER BIN POINT, OBSERVED FREQUENCY, AND EXPECTED FREQUENCY
WRITTEN TO FILE DPST1F.DAT
CHI-SQUARED GOODNESS-OF-FIT TEST
NULL HYPOTHESIS H0: DISTRIBUTION FITS THE DATA
ALTERNATE HYPOTHESIS HA: DISTRIBUTION DOES NOT FIT THE DATA
DISTRIBUTION: ZETA
SAMPLE:
NUMBER OF OBSERVATIONS = 500
NUMBER OF NON-EMPTY CELLS = 9
NUMBER OF PARAMETERS USED = 1
TEST:
CHI-SQUARED TEST STATISTIC = 5.979143
DEGREES OF FREEDOM = 7
CHI-SQUARED CDF VALUE = 0.457813
ALPHA LEVEL CUTOFF CONCLUSION
10% 12.01704 ACCEPT H0
5% 14.06714 ACCEPT H0
1% 18.47531 ACCEPT H0
CELL NUMBER, LOWER BIN POINT, UPPER BIN POINT, OBSERVED FREQUENCY, AND EXPECTED FREQUENCY
WRITTEN TO FILE DPST1F.DAT
Date created: 6/5/2006
Last updated: 6/5/2006
Please email comments on this WWW page to
alan.heckert@nist.gov.
|


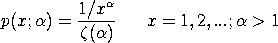
![zeta(alpha) = SUM[i=t to infinity][1/x**alpha]](eqns/zetafunc.gif)