
|
Main MCMC Page |
mcmc03 Dataset |
mcmc03 Results |
|---|
-
The joint density for data
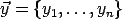 , given the parameters
, given the parameters
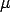 and
and  is
is
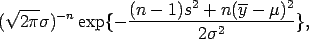
with sample mean,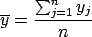 ,
and sample variance,
,
and sample variance, 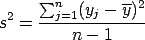 .
.
The joint prior density for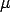 and
and  is
proportional to
is
proportional to 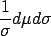 (a non-informative prior specification).
(a non-informative prior specification).
- For all datasets, extended precision calculations (accurate to 500 digits) were made. Data were read in exactly as extended precision numbers and all calculations were made with this very high precision. The results were output in extended precision, and only then rounded to fifteen decimal places. These extended precision results are an idealization. They represent what would be achieved if calculations were made without roundoff or other numerical errors. Any typical numerical algorithm (i.e., not implemented in extended precision) will introduce computational inaccuracies, and will produce results which differ slightly from these certified values.
-
- Using Bayes' Theorem, the joint posterior probability density of
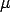 and
and  , given
, given
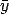 and
and 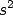 is
is
![\pi (\mu, \sigma |\overline y, s^2) =
C\sigma^{-(n+1)} \exp [-\frac{n(\mu - \overline y)^2}{2\sigma^2}
- \frac{(n-1)s^2}{2\sigma^2}],](eqns/eq10.gif)
where the normalizing constant
![C = \sqrt\frac{2n}{\pi} [\Gamma((n-1)/2)]^{-1}\left[\frac{(n-1) s^2}{2}\right]^{(n-1)/2},](eqns/eq11.gif)
and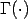 is the gamma function defined by
is the gamma function defined by
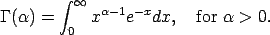
It is convenient to denote the marginal posterior distribution of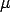 by
by
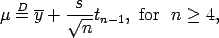
where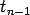 denotes a random variable with
a Student's t distribution with
denotes a random variable with
a Student's t distribution with 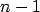 degrees of freedom, and the symbol
degrees of freedom, and the symbol
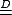 denotes equal in distribution.
denotes equal in distribution.
Similarly the marginal posterior distribution of can be denoted by
can be denoted by
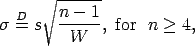
where W is a chi-square random variable with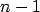 degrees of freedom.
degrees of freedom.
- The posterior mean of
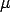
The certified value of the posterior mean of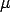 is defined by
is defined by
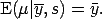
- The posterior standard deviation of
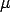
The certified value of the posterior standard deviation of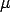 is defined by
is defined by
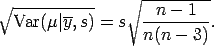
- The
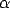 th posterior quantile of
th posterior quantile of 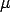
The certified value of the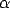 th posterior
quantile of
th posterior
quantile of 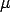 is defined by
is defined by
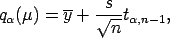 where
where 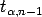 is the
is the 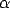 th quantile of a t distribution
with
th quantile of a t distribution
with 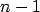 degrees of freedom.
degrees of freedom.
- The posterior mean of

The certified value of the posterior mean of is defined by
is defined by
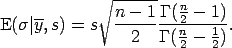
- The posterior standard deviation of

The certified value of the posterior standard deviation of is defined by
is defined by
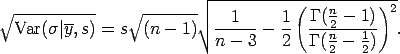
- The
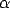 th posterior quantile of
th posterior quantile of 
The certified value of the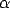 th posterior
quantile of
th posterior
quantile of  is defined by
is defined by
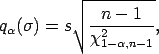 where
where 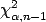 is the
is the 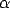 th quantile of a chi-square distribution
with
th quantile of a chi-square distribution
with 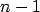 degrees of freedom.
degrees of freedom.
- Using Bayes' Theorem, the joint posterior probability density of