8.1. Introduction
8.1.3. What are some common difficulties with reliability data and how are they overcome?
8.1.3.1. |
Censoring |
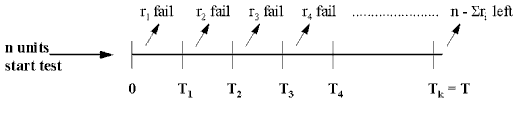
Consider a situation in which we are reliability testing \(n\) (non-repairable) units taken randomly from a population. We are investigating the population to determine if its failure rate is acceptable. In the typical test scenario, we have a fixed time \(T\) to run the units to see if they survive or fail. The data obtained are called Censored Type I data.
During the \(T\) hours of test we observe \(r\) failures (where \(r\) can be any number from 0 to \(n\)). The (exact) failure times are \(t_1, \, t_2, \, \ldots, \, t_r\), and there are \((n - r)\) units that survived the entire \(T\)-hour test without failing. Note that \(T\) is fixed in advance and \(r\) is random, since we don't know how many failures will occur until the test is run. Note also that we assume the exact times of failure are recorded when there are failures.
This type of censoring is also called "right censored" data since the times of failure to the right (i.e., larger than \(T\)) are missing.
Another (much less common) way to test is to decide in advance that you want to see exactly \(r\) failure times and then test until they occur. For example, you might put 100 units on test and decide you want to see at least half of them fail. Then \(r = 50\), but \(T\) is unknown until the 50th failure occurs. This is called Censored Type II data.
Censored Type II Data
We observe \(t_1, \, t_2, \, \ldots, \, t_r\), where \(r\) is specified in advance. The test ends at time \(T = t_r\), and \((n - r)\) units have survived. Again we assume it is possible to observe the exact time of failure for failed units.
Type II censoring has the significant advantage that you know in advance how many failure times your test will yield - this helps enormously when planning adequate tests. However, an open-ended random test time is generally impractical from a management point of view and this type of testing is rarely seen.
Sometimes exact times of failure are not known; only an interval of time in which the failure occurred is recorded. This kind of data is called Readout or Interval data and the situation is shown in the figure below:
In the most general case, every unit observed yields exactly one of the following three types of information:
- a run-time if the unit did not fail while under observation
- an exact failure time
- an interval of time during which the unit failed.
Many statistical methods can be used to fit models and estimate failure rates, even with censored data. In later sections we will discuss the Kaplan-Meier approach, Probability Plotting, Hazard Plotting, Graphical Estimation, and Maximum Likelihood Estimation.
Note that when a data set consists of failure times that can be sorted into several different failure modes, it is possible (and often necessary) to analyze and model each mode separately. Consider all failures due to modes other than the one being analyzed as censoring times, with the censored run-time equal to the time it failed due to the different (independent) failure mode. This is discussed further in the competing risk section and later analysis sections.

