1.3. EDA Techniques
1.3.6. Probability Distributions
1.3.6.6. Gallery of Distributions
1.3.6.6.15. |
Tukey-Lambda Distribution |
The Tukey-Lambda distribution has the shape parameter λ. As with other probability distributions, the Tukey-Lambda distribution can be transformed with a location parameter, μ, and a scale parameter, σ. Since the general form of probability functions can be expressed in terms of the standard distribution, all subsequent formulas in this section are given for the standard form of the function.
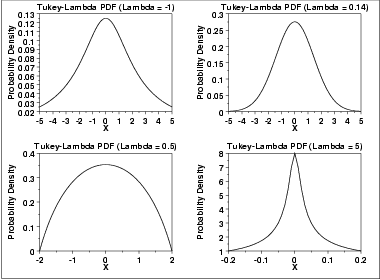
The following is the plot of the Tukey-Lambda probability density function for four values of λ.
The following is the plot of the Tukey-Lambda cumulative distribution function with the same values of λ as the pdf plots above.
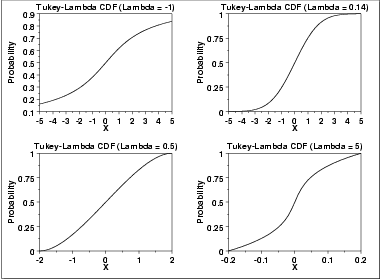
\( G(p;\lambda) = \frac{p^{\lambda} - (1 - p)^{\lambda}} {\lambda} \)
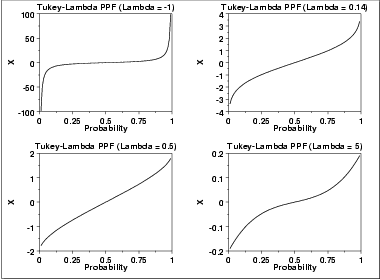
The following is the plot of the Tukey-Lambda percent point function with the same values of λ as the pdf plots above.
| λ = -1 | approximately Cauchy |
| λ = 0 | exactly logistic |
| λ = 0.14 | approximately normal |
| λ = 0.5 | U-shaped |
| λ = 1 | exactly uniform (from -1 to +1) |
The most common use of this distribution is to generate a Tukey-Lambda PPCC plot of a data set. Based on the ppcc plot, an appropriate model for the data is suggested. For example, if the maximum correlation occurs for a value of λ at or near 0.14, then the data can be modeled with a normal distribution. Values of λ less than this imply a heavy-tailed distribution (with -1 approximating a Cauchy). That is, as the optimal value of λ goes from 0.14 to -1, increasingly heavy tails are implied. Similarly, as the optimal value of λ becomes greater than 0.14, shorter tails are implied.
As the Tukey-Lambda distribution is a symmetric distribution, the use of the Tukey-Lambda PPCC plot to determine a reasonable distribution to model the data only applies to symmetric distributions. A histogram of the data should provide evidence as to whether the data can be reasonably modeled with a symmetric distribution.

