3. Production Process Characterization
3.4. Data Analysis for PPC

3.4.6.

Assessing Process Capability

Capability compares a process against its specification

Process capability analysis entails comparing the performance of a process against its specifications. We say that a process is capable if virtually all of the possible variable values fall within the specification limits.

Use a capability chart

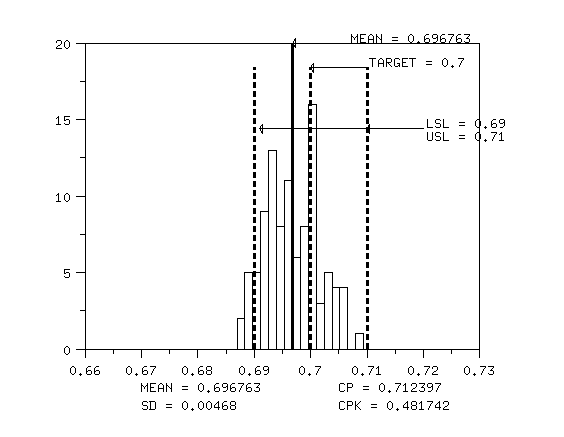
Graphically, we assess process capability by plotting the process specification limits on a histogram of the observations. If the histogram falls within the specification limits, then the process is capable. This is illustrated in the graph below. Note how the process is shifted below target and the process variation is too large. This is an example of an incapable process.

Notice how the process is off target and has too much variation

Numerically, we measure capability with a capability index. The general equation for the capability index, C_p, is:

Numerically, we use the C_p index

\( C_{p} = \frac{\mbox{USL} - \mbox{LSL}}{6s} \)

Interpretation of the C_p index

This equation just says that the measure of our process capability is how much of our observed process variation is covered by the process specifications. In this case the process variation is measured by 6 standard deviations (+/- 3 on each side of the mean). Clearly, if C_p > 1.0, then the process specification covers almost all of our process observations.

C_p does not account for process that is off center

The only problem with with the C_p index is that it does not account for a process that is off-center. We can modify this equation slightly to account for off-center processes to obtain the C_pk index as follows:

Or the C_pk index

\( C_{pk} = \min \left[ \frac{\mbox{USL} - \bar{x}}{3s}, \frac{\bar{x} - \mbox{LSL}}{3s} \right] \)

C_pk accounts for a process being off center

This equation just says to take the minimum distance between our specification limits and the process mean and divide it by 3 standard deviations to arrive at the measure of process capability. This is all covered in more detail in the process capability section of the process monitoring chapter. For the example above, note how the C_pk value is less than the C_p value. This is because the process distribution is not centered between the specification limits.