

|
PARTIAL REGRESSION PLOTName:
Partial regression plots attempt to show the effect of adding an additional variable to the model (given that one or more independent variables are already in the model). Partial regression plots are formed by:
Velleman and Welsch (see References below) express this mathematically as:
where
Xi.[i] = residuals from regressing Xi against the remaining indpependent variables. Velleman and Welsch list the following useful properties for this plot:
Partial regression plots are widely discussed in the regression diagnostics literature (e.g., see the References section below). Since the strengths and weaknesses of partial regression plots are widely discussed in the literature, we will not discuss that in any detail here. Partial regression plots are related to, but distinct from, partial residual plots. Partial regression plots are most commonly used to identify leverage points and influential data points that might not be leverage points. Partial residual plots are most commonly used to identify the nature of the relationship between Y and Xi (given the effect of the other independent variables in the model). Note that since the simple correlation betweeen the two sets of residuals plotted is equal to the partial correlation between the response variable and Xi partial regression plots will show the correct strength of the linear relationship between the response variable and Xi This is not true for partial residual plots. On the other hand, for the partial regression plot, the x axis is not Xi. This limits its usefulness in determining the need for a transformation (which is the primary purpose of the partial residual plot). Dataplot provides two forms for the partial regression plot. You can generate either a single partial regression plot or you can generate a matrix of partial regression plots (one plot for each independent variable in the model). For the matrix form of the command, a number of SET FACTOR PLOT options can be used to control the appearance of the plot (not all of the SET FACTOR PLOT options apply). These are discussed in the Notes section below.
<SUBSET/EXCEPT/FOR qualification> where <y> is the response variable; <x1> ... <xk> are the independent variables; <xi> is the independent variable for which the partial regression plot is being generated (note that <xi> must be one of the variables listed in <x1> ... <xk>; and where the <SUBSET/EXCEPT/FOR qualification> is optional. This is the syntax for generating a single partial regression plot.
<SUBSET/EXCEPT/FOR qualification> where <y> is the response variable; <x1> ... <xk> are the independent variables; and where the <SUBSET/EXCEPT/FOR qualification> is optional. This syntax is used to generate a matrix of partial regression plots.
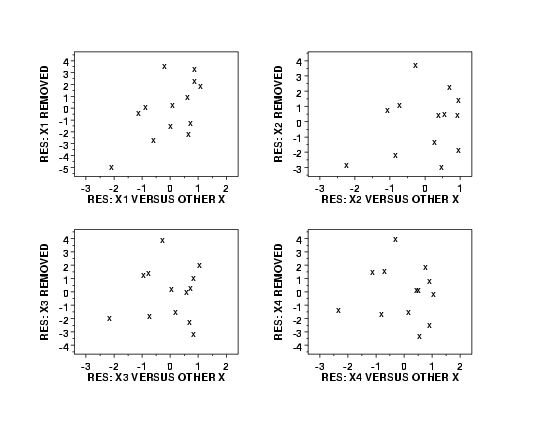
MATRIX PARTIAL REGRESSION PLOT Y X1 X2 X3 X4
PARTIAL REGRESSION PLOT Y X1 X2 X3 X4 X2 SUBSET TAG > 2
OFF means that all axis labels are suppressed (this can be useful if a large number of variables are being plotted). ON means that both X and Y axis labels are printed. XON only plots the x axis labels and YON only plots the y axis labels. BOX is a special option that creates an extra column on the left and an extra row on the bottom. The axis label is printed in this box. BOX is typically reserved for the plot types that plot the variable names in the axes labels. The default is ON (both x and y axis labels are printed).
BOTTOM specifies that the x axis labels are printed on the bottom axis (on the last row only). TOP specifies that the x axis labels are printed on the top axis (first row only). ALTERNATE specifies that the x axis labels alternate between the top (first row) and bottom axis (last row). We recommend using the TIC OFFSET command to avoid overlap of axis labels and tic marks. The default is ALTERNATE.
LEFT specifies that the y axis labels are printed on the left axis (on the first column only). RIGHT specifies that the y axis labels are printed on the right axis (last column only). ALTERNATE specifies that the y axis labels alternate between the left (first column) and right axis (last column). We recommend using the TIC OFFSET command to avoid overlap of axis labels and tic marks. The default is ALTERNATE.
DEFAULT connects neighboring frames (i.e., the FRAME CORNER
COORDINATES are set to 0 0 100 100). USER uses whatever
frame coordinates are currently set (15 20 85 90 by default)
and makes no special provisions for axis labels and tic marks
(i.e., you set them as you normally would, each plot uses
whatever you have set). CONNECTED uses whatever frame
coordinates have been set by the user, but it draws the axis
labels and tic marks as if DEFAULT were being used (that is, as
determined by the SET FACTOR PLOT
Since the plots can often have different limits for the axes,
the default is USER.
NORMAL means that all tic labels are plotted at a distance determined by the TIC LABEL DISPLACEMENT command. STAGGERED means that alternating plots will be staggered. That is, one will use the standard displacement while the next uses a staggered value. Entering this command with a numeric value specifies the amount of the displacement for the staggered tic labels. For example,
SET FACTOR PLOT LABEL DISPLACEMENT STAGGERED SET FACTOR PLOT LABEL DISPLACEMENT 25 These commands specify that the default tic label displacement is 10 and the staggered tic mark label displacement is 25.
NONE means that no fitted line is plotted. LOWESS means that a locally weighted least squares line will be overlaid. LINE means that a linear fit (Y = A0 + A1*X) will be overlaid. QUAD means that a quadratic fit (Y = A0 + A1*X + A2*X**2) will be overlaid. SMOOTH means that a least squares smoothing will be overlaid. For LOWESS, it is recommended that the lowess fraction be set fairly high (e.g., LOWESS FRACTION 0.6). The fitted line is currently only generated if the factor plot type is PLOT. The default is for no fitted line to be overlaid on the plot. If a overlaid fit is desired, the most common choice is to use LOWESS.
SET FACTOR PLOT XLIMITS <LOW1> <UPP1> <LOW2> <UPP2> ... The default is to allow the axis limits to float with the data.
For example,
MULTIPLOT SCALE FACTOR 3 TIC OFFSET UNITS SCREEN TIC OFFSET 5 5
Neter, Wasserman, and Kunter (1990), "Applied Linear Statistical Models", 3rd ed., Irwin. Draper and Smith (1998), "Applied Regression Analysis", 3rd. ed., John Wiley. Cook and Weisberg (1982), "Residuals and Influence in Regression", Chapman and Hall. Belsley, Kuh, and Welsch (1980), "Regression Diagnostics", John Wiley. Velleman and Welsch (1981), "Efficient Computing of Regression Diagnostiocs", The American Statistician, Vol. 35, No. 4, pp. 234-242.
SKIP 25
READ HALD647.DAT Y X1 X2 X3 X4
.
MULTIPLOT CORNER COORDINATES 5 5 95 95
MULTIPLOT SCALE FACTOR 2
LINE BLANK
CHARACTER X
X1LABEL DISPLACEMENT 12
Y1LABEL DISPLACEMENT 12
TIC OFFSET UNITS SCREEN
TIC OFFSET 5 5
.
MATRIX PARTIAL REGRESSION PLOT Y X1 X2 X3 X4
Date created: 08/19/2002 |
Last updated: 12/04/2023 Please email comments on this WWW page to alan.heckert@nist.gov. | ||||||||||||||||||||||