PARTIAL RESIDUAL PLOT

PARTIAL RESIDUAL PLOT

Graphics Command

Generate a partial residual plot.

When performing a linear regression with a single independent variable, a scatter plot of the response variable against the independent variable provides a good indication of the nature of the relationship. If there is more than one independent variable, things become more complicated. Although it can still be useful to generate scatter plots of the response variable against each of the independent variables, this does not take into account the effect of the other independent variables in the model.

Partial residual plots attempt to show the relationship between a given independent variable and the response variable given that other independent variables are also in the model.

Partial residual plots are formed as:

\( \mbox{Res} + \hat{\beta}_{i} X_{i} \) versus \( X_{i} \)

where

Res = residuals from the full model
\( \hat{\beta}_{i} \) = regression coefficient from the ith independent variable in the full model
X_i = the i-th independent variable


Partial residual plots are widely discussed in the regression diagnostics literature (e.g., see the References section below). Although they can often be useful, be aware that they can also fail to indicate the proper relationship. In particular, if X_i is highly correlated with any of the other independent variables, the variance indicated by the partial residual plot can be much less than the actual variance. These issues are discussed in more detail in the references given below.

Dataplot provides two forms for the partial residual plot. You can generate either a single partial residual plot or you can generate a matrix of partial residual plots (one plot for each independent variable in the model).

For the matrix form of the command, a number of SET FACTOR PLOT options can be used to control the appearance of the plot (not all of the SET FACTOR PLOT options apply). These are discussed in the Notes section below.

The CCPR plot is a variation of the PARTIAL RESIDUAL PLOT. Enter HELP CCPR PLOT for details.

PARTIAL RESIDUAL PLOT <y> <x1> ... <xk> <xi>
                            <SUBSET/EXCEPT/FOR qualification>
where <y> is the response variable;
              <x1> ... <xk> are the independent variables;
              <xi> is the independent variable for which the partial residual plot is being generated
                            (note that <xi> must be one of the variables listed in <x1> ... <xk>;
and where the <SUBSET/EXCEPT/FOR qualification> is optional.

This is the syntax for generating a single partial residual plot.

MATRIX PARTIAL RESIDUAL PLOT <y> <x1> ... <xk>
                            <SUBSET/EXCEPT/FOR qualification>
where <y> is the response variable;
              <x1> ... <xk> are the independent variables;
and where the <SUBSET/EXCEPT/FOR qualification> is optional.

This syntax is used to generate a matrix of partial residual plots.

PARTIAL RESIDUAL PLOT Y X1 X2 X3 X4 X2


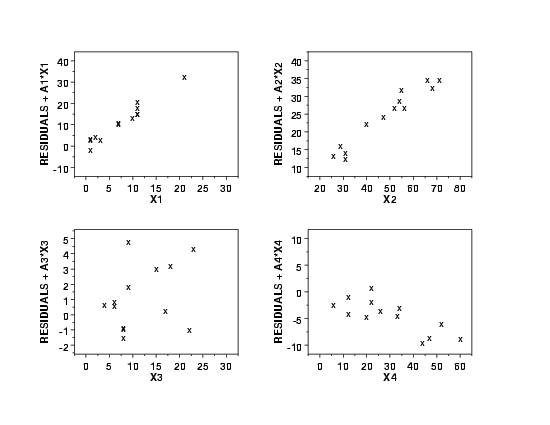
MATRIX PARTIAL RESIDUAL PLOT Y X1 X2 X3 X4


PARTIAL RESIDUAL PLOT Y X1 X2 X3 X4 X2 SUBSET TAG > 2
MATRIX PARTIAL RESIDUAL PLOT Y X1 X2 X3 X4 SUBSET TAG > 2

None

None

FIT	= Perform a multi-linear fit.
PARTIAL LEVERAGE PLOT	= Generates a partial leverage plot.
PARTIAL REGRESSION PLOT	= Generates a partial regression plot.
CCPR PLOT	= Generates a CCPR plot.
VIF	= Compute variance inflation factors for a multi-linear fit.
CONDITION INDICES	= Compute condition indices for a design matrix.
SCATTER PLOT MATIRX	= Generate a factor plot.
FACTOR PLOT	= Generate a plot for a response against a number of different independent variables.
CONDITIONAL PLOT	= Generate a conditional (subset) plot.

Tom Ryan (1997), "Modern Regression Methods", John Wiley.

Neter, Wasserman, and Kunter (1990), "Applied Linear Statistical Models", 3rd ed., Irwin.

Draper and Smith (1998), "Applied Regression Analysis", 3rd. ed., John Wiley.

Cook and Weisberg (1982), "Residuals and Influence in Regression", Chapman and Hall.

Belsley, Kuh, and Welsch (1980), "Regression Diagnostics", John Wiley.

Velleman and Welsch (1981), "Efficient Computing of Regression Diagnostiocs", The American Statistician, Vol. 35, No. 4, pp. 234-242.

Multi-linear Regression

2002/6

SKIP 25
READ HALD647.DAT Y X1 X2 X3 X4
.
MULTIPLOT CORNER COORDINATES 5 5 95 95
MULTIPLOT SCALE FACTOR 2
LINE BLANK
CHARACTER X
X1LABEL DISPLACEMENT 12
Y1LABEL DISPLACEMENT 12
TIC OFFSET UNITS SCREEN
TIC OFFSET 5 5
.
MATRIX PARTIAL RESIDUAL PLOT Y X1 X2 X3 X4