1.3. EDA Techniques
1.3.3. Graphical Techniques: Alphabetic
1.3.3.12. |
DOE Mean Plot |
Detect Important Factors With Respect to Location
This plot is typically generated for the mean. However, it can be generated for other location statistics such as the median.
Factors 4, 2, and 1 Are the Most Important Factors
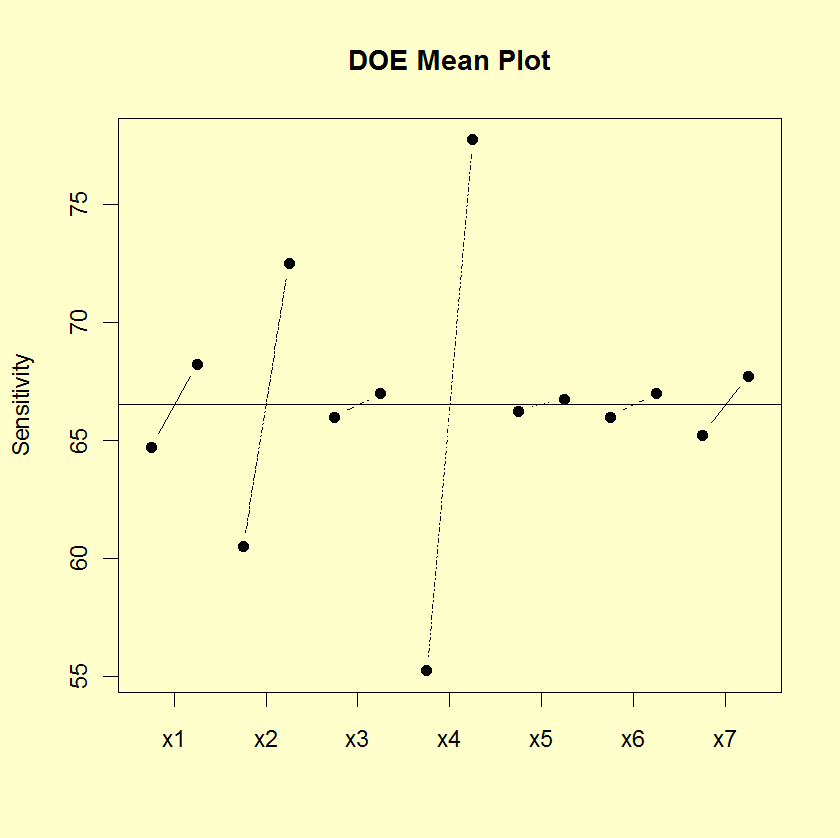
This sample DOE mean plot of the BOXBIKE2.DAT data set shows that:
- factor 4 is the most important;
- factor 2 is the second most important;
- factor 1 is the third most important;
- factor 7 is the fourth most important;
- factor 6 is the fifth most important;
- factors 3 and 5 are relatively unimportant.
Mean Response Versus Factor Variables
- Vertical axis: Mean of the response variable for each level of the factor
- Horizontal axis: Factor variable
- Which factors are important? The DOE mean plot does not provide a definitive answer to this question, but it does help categorize factors as "clearly important", "clearly not important", and "borderline importance".
- What is the ranking list of the important factors?
Determine Significant Factors
Specifically, if there are k factors, we create a matrix of plots with k rows and k columns. On the diagonal, the plot is simply a DOE mean plot with a single factor. For the off-diagonal plots, measurements at each level of the interaction are plotted versus level, where level is Xi times Xj and Xi is the code for the ith main effect level and Xj is the code for the jth main effect. For the common 2-level designs (i.e., each factor has two levels) the values are typically coded as -1 and 1, so the multiplied values are also -1 and 1. We then generate a DOE mean plot for this interaction variable. This plot is called a DOE interaction effects plot and an example is shown below.
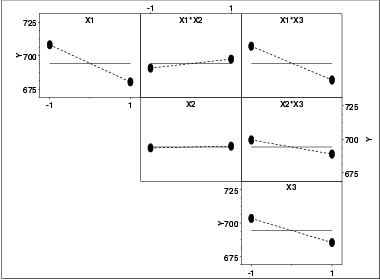
This plot shows that the most significant factor is X1 and the most significant interaction is between X1 and X3.
DOE standard deviation plot
Block plot
Box plot
Analysis of variance

