1.3. EDA Techniques
1.3.6. Probability Distributions
1.3.6.6. Gallery of Distributions
1.3.6.6.1. |
Normal Distribution |
\( f(x) = \frac{e^{-(x - \mu)^{2}/(2\sigma^{2}) }} {\sigma\sqrt{2\pi}} \)
where μ is the location parameter and σ is the scale parameter. The case where μ = 0 and σ = 1 is called the standard normal distribution. The equation for the standard normal distribution is
\( f(x) = \frac{e^{-x^{2}/2}} {\sqrt{2\pi}} \)
Since the general form of probability functions can be expressed in terms of the standard distribution, all subsequent formulas in this section are given for the standard form of the function.
The following is the plot of the standard normal probability density function.
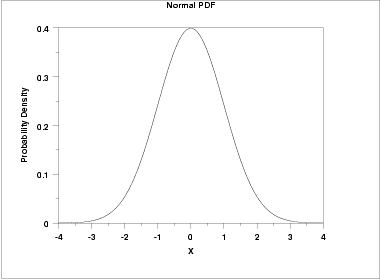
\( F(x) = \int_{-\infty}^{x} \frac{e^{-x^{2}/2}} {\sqrt{2\pi}} \)
Note that this integral does not exist in a simple closed formula. It is computed numerically.
The following is the plot of the normal cumulative distribution function.
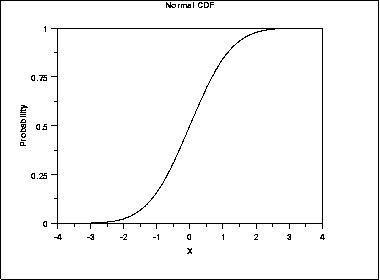
The following is the plot of the normal percent point function.
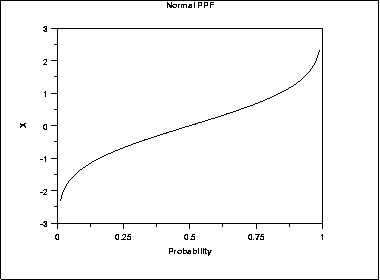
\( h(x) = \frac{\phi(x)} {\Phi(-x)} \)
where \(\Phi\) is the cumulative distribution function of the standard normal distribution and \(\phi\) is the probability density function of the standard normal distribution.
The following is the plot of the normal hazard function.
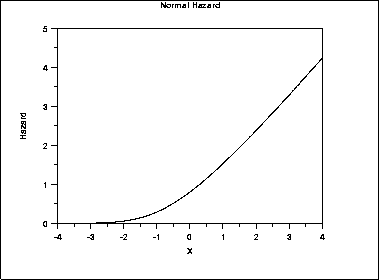
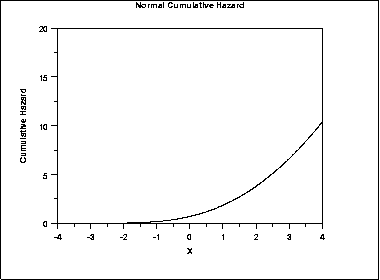
The following is the plot of the normal cumulative hazard function.
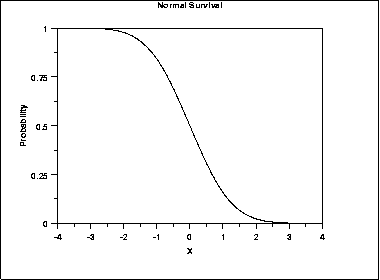
The following is the plot of the normal survival function.
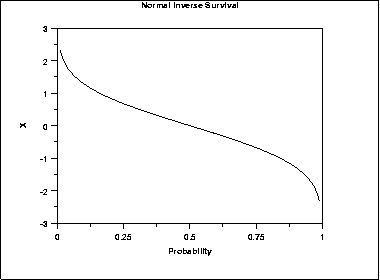
The following is the plot of the normal inverse survival function.
| Mean | The location parameter μ. |
| Median | The location parameter μ. |
| Mode | The location parameter μ. |
| Range | \(-\infty\) to \(\infty\). |
| Standard Deviation | The scale parameter σ. |
| Coefficient of Variation | σ/μ |
| Skewness | 0 |
| Kurtosis | 3 |
- Many classical statistical tests are based on the assumption
that the data follow a normal distribution. This assumption
should be tested before applying these tests.
- In modeling applications, such as linear and non-linear
regression, the error term is often assumed to follow a normal
distribution with fixed location and scale.
- The normal distribution is used to find significance levels in many hypothesis tests and confidence intervals.
The central limit theorem basically states that as the sample size (N) becomes large, the following occur:
- The sampling distribution of the mean becomes approximately
normal regardless of the distribution of the original
variable.
- The sampling distribution of the mean is centered at the population mean, μ, of the original variable. In addition, the standard deviation of the sampling distribution of the mean approaches \( \sigma / \sqrt{N} \).

