1. Exploratory Data Analysis
1.3. EDA Techniques
1.3.6. Probability Distributions
1.3.6.7. Tables for Probability Distributions

1.3.6.7.4.

Critical Values of the Chi-Square Distribution

How to Use This Table

This table contains the critical values of the chi-square distribution. Because of the lack of symmetry of the chi-square distribution, separate tables are provided for the upper and lower tails of the distribution.

A test statistic with ν degrees of freedom is computed from the data. For upper-tail one-sided tests, the test statistic is compared with a value from the table of upper-tail critical values. For two-sided tests, the test statistic is compared with values from both the table for the upper-tail critical values and the table for the lower-tail critical values.

The significance level, α, is demonstrated with the graph below which shows a chi-square distribution with 3 degrees of freedom for a two-sided test at significance level α = 0.05. If the test statistic is greater than the upper-tail critical value or less than the lower-tail critical value, we reject the null hypothesis. Specific instructions are given below.

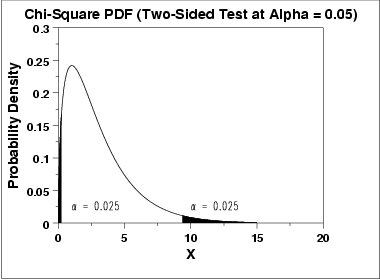
Given a specified value of α:

1. For a two-sided test, find the column corresponding to 1-α/2 in the table for upper-tail critical values and reject the null hypothesis if the test statistic is greater than the tabled value. Similarly, find the column corresponding to α/2 in the table for lower-tail critical values and reject the null hypothesis if the test statistic is less than the tabled value.
2. For an upper-tail one-sided test, find the column corresponding to 1-α in the table containing upper-tail critical and reject the null hypothesis if the test statistic is greater than the tabled value.
3. For a lower-tail one-sided test, find the column corresponding to α in the lower-tail critical values table and reject the null hypothesis if the computed test statistic is less than the tabled value.

Upper-tail critical values of chi-square distribution with ν degrees of freedom Probability less than the critical value ν 0.90 0.95 0.975 0.99 0.999 1 2.706 3.841 5.024 6.635 10.828 2 4.605 5.991 7.378 9.210 13.816 3 6.251 7.815 9.348 11.345 16.266 4 7.779 9.488 11.143 13.277 18.467 5 9.236 11.070 12.833 15.086 20.515 6 10.645 12.592 14.449 16.812 22.458 7 12.017 14.067 16.013 18.475 24.322 8 13.362 15.507 17.535 20.090 26.125 9 14.684 16.919 19.023 21.666 27.877 10 15.987 18.307 20.483 23.209 29.588 11 17.275 19.675 21.920 24.725 31.264 12 18.549 21.026 23.337 26.217 32.910 13 19.812 22.362 24.736 27.688 34.528 14 21.064 23.685 26.119 29.141 36.123 15 22.307 24.996 27.488 30.578 37.697 16 23.542 26.296 28.845 32.000 39.252 17 24.769 27.587 30.191 33.409 40.790 18 25.989 28.869 31.526 34.805 42.312 19 27.204 30.144 32.852 36.191 43.820 20 28.412 31.410 34.170 37.566 45.315 21 29.615 32.671 35.479 38.932 46.797 22 30.813 33.924 36.781 40.289 48.268 23 32.007 35.172 38.076 41.638 49.728 24 33.196 36.415 39.364 42.980 51.179 25 34.382 37.652 40.646 44.314 52.620 26 35.563 38.885 41.923 45.642 54.052 27 36.741 40.113 43.195 46.963 55.476 28 37.916 41.337 44.461 48.278 56.892 29 39.087 42.557 45.722 49.588 58.301 30 40.256 43.773 46.979 50.892 59.703 31 41.422 44.985 48.232 52.191 61.098 32 42.585 46.194 49.480 53.486 62.487 33 43.745 47.400 50.725 54.776 63.870 34 44.903 48.602 51.966 56.061 65.247 35 46.059 49.802 53.203 57.342 66.619 36 47.212 50.998 54.437 58.619 67.985 37 48.363 52.192 55.668 59.893 69.347 38 49.513 53.384 56.896 61.162 70.703 39 50.660 54.572 58.120 62.428 72.055 40 51.805 55.758 59.342 63.691 73.402 41 52.949 56.942 60.561 64.950 74.745 42 54.090 58.124 61.777 66.206 76.084 43 55.230 59.304 62.990 67.459 77.419 44 56.369 60.481 64.201 68.710 78.750 45 57.505 61.656 65.410 69.957 80.077 46 58.641 62.830 66.617 71.201 81.400 47 59.774 64.001 67.821 72.443 82.720 48 60.907 65.171 69.023 73.683 84.037 49 62.038 66.339 70.222 74.919 85.351 50 63.167 67.505 71.420 76.154 86.661 51 64.295 68.669 72.616 77.386 87.968 52 65.422 69.832 73.810 78.616 89.272 53 66.548 70.993 75.002 79.843 90.573 54 67.673 72.153 76.192 81.069 91.872 55 68.796 73.311 77.380 82.292 93.168 56 69.919 74.468 78.567 83.513 94.461 57 71.040 75.624 79.752 84.733 95.751 58 72.160 76.778 80.936 85.950 97.039 59 73.279 77.931 82.117 87.166 98.324 60 74.397 79.082 83.298 88.379 99.607 61 75.514 80.232 84.476 89.591 100.888 62 76.630 81.381 85.654 90.802 102.166 63 77.745 82.529 86.830 92.010 103.442 64 78.860 83.675 88.004 93.217 104.716 65 79.973 84.821 89.177 94.422 105.988 66 81.085 85.965 90.349 95.626 107.258 67 82.197 87.108 91.519 96.828 108.526 68 83.308 88.250 92.689 98.028 109.791 69 84.418 89.391 93.856 99.228 111.055 70 85.527 90.531 95.023 100.425 112.317 71 86.635 91.670 96.189 101.621 113.577 72 87.743 92.808 97.353 102.816 114.835 73 88.850 93.945 98.516 104.010 116.092 74 89.956 95.081 99.678 105.202 117.346 75 91.061 96.217 100.839 106.393 118.599 76 92.166 97.351 101.999 107.583 119.850 77 93.270 98.484 103.158 108.771 121.100 78 94.374 99.617 104.316 109.958 122.348 79 95.476 100.749 105.473 111.144 123.594 80 96.578 101.879 106.629 112.329 124.839 81 97.680 103.010 107.783 113.512 126.083 82 98.780 104.139 108.937 114.695 127.324 83 99.880 105.267 110.090 115.876 128.565 84 100.980 106.395 111.242 117.057 129.804 85 102.079 107.522 112.393 118.236 131.041 86 103.177 108.648 113.544 119.414 132.277 87 104.275 109.773 114.693 120.591 133.512 88 105.372 110.898 115.841 121.767 134.746 89 106.469 112.022 116.989 122.942 135.978 90 107.565 113.145 118.136 124.116 137.208 91 108.661 114.268 119.282 125.289 138.438 92 109.756 115.390 120.427 126.462 139.666 93 110.850 116.511 121.571 127.633 140.893 94 111.944 117.632 122.715 128.803 142.119 95 113.038 118.752 123.858 129.973 143.344 96 114.131 119.871 125.000 131.141 144.567 97 115.223 120.990 126.141 132.309 145.789 98 116.315 122.108 127.282 133.476 147.010 99 117.407 123.225 128.422 134.642 148.230 100 118.498 124.342 129.561 135.807 149.449 100 118.498 124.342 129.561 135.807 149.449 Lower-tail critical values of chi-square distribution with ν degrees of freedom Probability less than the critical value ν 0.10 0.05 0.025 0.01 0.001 1. .016 .004 .001 .000 .000 2. .211 .103 .051 .020 .002 3. .584 .352 .216 .115 .024 4. 1.064 .711 .484 .297 .091 5. 1.610 1.145 .831 .554 .210 6. 2.204 1.635 1.237 .872 .381 7. 2.833 2.167 1.690 1.239 .598 8. 3.490 2.733 2.180 1.646 .857 9. 4.168 3.325 2.700 2.088 1.152 10. 4.865 3.940 3.247 2.558 1.479 11. 5.578 4.575 3.816 3.053 1.834 12. 6.304 5.226 4.404 3.571 2.214 13. 7.042 5.892 5.009 4.107 2.617 14. 7.790 6.571 5.629 4.660 3.041 15. 8.547 7.261 6.262 5.229 3.483 16. 9.312 7.962 6.908 5.812 3.942 17. 10.085 8.672 7.564 6.408 4.416 18. 10.865 9.390 8.231 7.015 4.905 19. 11.651 10.117 8.907 7.633 5.407 20. 12.443 10.851 9.591 8.260 5.921 21. 13.240 11.591 10.283 8.897 6.447 22. 14.041 12.338 10.982 9.542 6.983 23. 14.848 13.091 11.689 10.196 7.529 24. 15.659 13.848 12.401 10.856 8.085 25. 16.473 14.611 13.120 11.524 8.649 26. 17.292 15.379 13.844 12.198 9.222 27. 18.114 16.151 14.573 12.879 9.803 28. 18.939 16.928 15.308 13.565 10.391 29. 19.768 17.708 16.047 14.256 10.986 30. 20.599 18.493 16.791 14.953 11.588 31. 21.434 19.281 17.539 15.655 12.196 32. 22.271 20.072 18.291 16.362 12.811 33. 23.110 20.867 19.047 17.074 13.431 34. 23.952 21.664 19.806 17.789 14.057 35. 24.797 22.465 20.569 18.509 14.688 36. 25.643 23.269 21.336 19.233 15.324 37. 26.492 24.075 22.106 19.960 15.965 38. 27.343 24.884 22.878 20.691 16.611 39. 28.196 25.695 23.654 21.426 17.262 40. 29.051 26.509 24.433 22.164 17.916 41. 29.907 27.326 25.215 22.906 18.575 42. 30.765 28.144 25.999 23.650 19.239 43. 31.625 28.965 26.785 24.398 19.906 44. 32.487 29.787 27.575 25.148 20.576 45. 33.350 30.612 28.366 25.901 21.251 46. 34.215 31.439 29.160 26.657 21.929 47. 35.081 32.268 29.956 27.416 22.610 48. 35.949 33.098 30.755 28.177 23.295 49. 36.818 33.930 31.555 28.941 23.983 50. 37.689 34.764 32.357 29.707 24.674 51. 38.560 35.600 33.162 30.475 25.368 52. 39.433 36.437 33.968 31.246 26.065 53. 40.308 37.276 34.776 32.018 26.765 54. 41.183 38.116 35.586 32.793 27.468 55. 42.060 38.958 36.398 33.570 28.173 56. 42.937 39.801 37.212 34.350 28.881 57. 43.816 40.646 38.027 35.131 29.592 58. 44.696 41.492 38.844 35.913 30.305 59. 45.577 42.339 39.662 36.698 31.020 60. 46.459 43.188 40.482 37.485 31.738 61. 47.342 44.038 41.303 38.273 32.459 62. 48.226 44.889 42.126 39.063 33.181 63. 49.111 45.741 42.950 39.855 33.906 64. 49.996 46.595 43.776 40.649 34.633 65. 50.883 47.450 44.603 41.444 35.362 66. 51.770 48.305 45.431 42.240 36.093 67. 52.659 49.162 46.261 43.038 36.826 68. 53.548 50.020 47.092 43.838 37.561 69. 54.438 50.879 47.924 44.639 38.298 70. 55.329 51.739 48.758 45.442 39.036 71. 56.221 52.600 49.592 46.246 39.777 72. 57.113 53.462 50.428 47.051 40.519 73. 58.006 54.325 51.265 47.858 41.264 74. 58.900 55.189 52.103 48.666 42.010 75. 59.795 56.054 52.942 49.475 42.757 76. 60.690 56.920 53.782 50.286 43.507 77. 61.586 57.786 54.623 51.097 44.258 78. 62.483 58.654 55.466 51.910 45.010 79. 63.380 59.522 56.309 52.725 45.764 80. 64.278 60.391 57.153 53.540 46.520 81. 65.176 61.261 57.998 54.357 47.277 82. 66.076 62.132 58.845 55.174 48.036 83. 66.976 63.004 59.692 55.993 48.796 84. 67.876 63.876 60.540 56.813 49.557 85. 68.777 64.749 61.389 57.634 50.320 86. 69.679 65.623 62.239 58.456 51.085 87. 70.581 66.498 63.089 59.279 51.850 88. 71.484 67.373 63.941 60.103 52.617 89. 72.387 68.249 64.793 60.928 53.386 90. 73.291 69.126 65.647 61.754 54.155 91. 74.196 70.003 66.501 62.581 54.926 92. 75.100 70.882 67.356 63.409 55.698 93. 76.006 71.760 68.211 64.238 56.472 94. 76.912 72.640 69.068 65.068 57.246 95. 77.818 73.520 69.925 65.898 58.022 96. 78.725 74.401 70.783 66.730 58.799 97. 79.633 75.282 71.642 67.562 59.577 98. 80.541 76.164 72.501 68.396 60.356 99. 81.449 77.046 73.361 69.230 61.137 100. 82.358 77.929 74.222 70.065 61.918