6.3.3.1. Counts Control Charts

6. Process or Product Monitoring and Control
6.3. Univariate and Multivariate Control Charts
6.3.3. What are Attributes Control Charts?

6.3.3.1. Counts Control Charts

Defective items vs individual defects

The literature differentiates between defect and defective, which is the same as differentiating between nonconformity and nonconforming units. This may sound like splitting hairs, but in the interest of clarity let's try to unravel this man-made mystery.

Consider a wafer with a number of chips on it. The wafer is referred to as an "item of a product". The chip may be referred to as "a specific point". There exist certain specifications for the wafers. When a particular wafer (e.g., the item of the product) does not meet at least one of the specifications, it is classified as a nonconforming item. Furthermore, each chip, (e.g., the specific point) at which a specification is not met becomes a defect or nonconformity.

So, a nonconforming or defective item contains at least one defect or nonconformity. It should be pointed out that a wafer can contain several defects but still be classified as conforming. For example, the defects may be located at noncritical positions on the wafer. If, on the other hand, the number of the so-called "unimportant" defects becomes alarmingly large, an investigation of the production of these wafers is warranted.

Control charts involving counts can be either for the total number of nonconformities (defects) for the sample of inspected units, or for the average number of defects per inspection unit.

Poisson approximation for numbers or counts of defects

Let us consider an assembled product such as a microcomputer. The opportunity for the occurrence of any given defect may be quite large. However, the probability of occurrence of a defect in any one arbitrarily chosen spot is likely to be very small. In such a case, the incidence of defects might be modeled by a Poisson distribution. Actually, the Poisson distribution is an approximation of the binomial distribution and applies well in this capacity according to the following rule of thumb:

The sample size $n$ should be equal to or larger than 20 and the probability of a single success, $p$, should be smaller than or equal to 0.05. If $n \ge 100$, the approximation is excellent if $np$ is also $\le 10$.

Illustrate Poisson approximation to binomial

To illustrate the use of the Poisson distribution as an approximation of a binomial distribution, consider the following comparison: Let $p$, the probability of a single success in $n = 200$ trials, be 0.025.

Find the probability of exactly 3 successes. If we assume that $p$ remains constant then the solution follows the binomial distribution rules, that is:

$ p(x) = \left( \begin{array}{c} n \\ x \end{array} \right) p^{x}(1 - p)^{n-x} = \left( \begin{array}{c} 200 \\ 3 \end{array} \right) (0.025^{3})(0.975^{197}) = 0.1399995 \, . $

By the Poisson approximation we have

$$ c = 200(0.025) $$ and

$$ p(x) = \frac{e^{-c}c^{x}}{x!} = \frac{e^{-5}5^{3}}{3!} = 0.1403739 \, .$$

The inspection unit

Before the control chart parameters are defined there is one more definition: the inspection unit. We shall count the number of defects that occur in a so-called inspection unit. More often than not, an inspection unit is a single unit or item of product; for example, a wafer. However, sometimes the inspection unit could consist of five wafers, or ten wafers and so on. The size of the inspection units may depend on the recording facility, measuring equipment, operators, etc.

Suppose that defects occur in a given inspection unit according to the Poisson distribution, with parameter $c$ (often denoted by $np$ or the Greek letter $\lambda$). In other words

Control charts for counts, using the Poisson distribution

$$ p(x) = \frac{e^{-c}c^{x}}{x!} \, ,$$

where $x$ is the number of defects and $c > 0$ is the parameter of the Poisson distribution. It is known that both the mean and the variance of this distribution are equal to $c$. Then the $k$-sigma control chart is $$ \begin{eqnarray} UCL & = & c + k\sqrt{c} \\ \mbox{Center Line} & = & c \\ LCL & = & c - k\sqrt{c} \, . \end{eqnarray} $$

If the $LCL$ comes out negative, then there is no lower control limit. This control scheme assumes that a standard value for $c$ is available. If this is not the case then $c$ may be estimated as the average of the number of defects in a preliminary sample of inspection units, call it $\bar{c}$. Usually $k$ is set to 3 by many practioners.

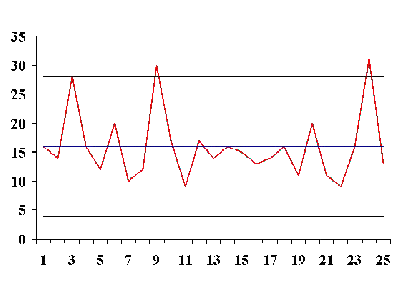
Control chart example using counts

An example may help to illustrate the construction of control limits for counts data. We are inspecting 25 successive wafers, each containing 100 chips; the wafer is the inspection unit. The observed number of defects are


Wafer	Number	Wafer	Number
Number	of Defects	Number	of Defects

1	16	14	16
2	14	15	15
3	28	16	13
4	16	17	14
5	12	18	16
6	20	19	11
7	10	20	20
8	12	21	11
9	10	22	19
10	17	23	16
11	19	24	31
12	17	25	13
13	14

The reader can download the data as a text file.

From this table we have

$$ UCL = \bar{c} + 3 \sqrt{\bar{c}} = 16 + 3 \sqrt{16} = 28 $$

$$ LCL = \bar{c} - 3 \sqrt{\bar{c}} = 16 - 3 \sqrt{16} = 4 \, . $$

Sample counts control chart

Control Chart for Counts

Sample counts control chart

	Transforming Poisson Data
Normal approximation to Poisson is adequate when the mean of the Poisson is at least 5	We have seen that the 3-sigma limits for a $c$ chart, where $c$ represents the number of nonconformities, are given by $$ \bar{c} \pm 3 \sqrt{\bar{c}} \, , $$ where it is assumed that the normal approximation to the Poisson distribution holds, hence the symmetry of the control limits. It is shown in the literature that the normal approximation to the Poisson is adequate when the mean of the Poisson is at least 5. When applied to the $c$ chart this implies that the mean of the defects should be at least 5. This requirement will often be met in practice, but still, when the mean is smaller than 9 (solving the above equation) there will be no lower control limit. Let the mean be 10. Then the lower control limit is 0.513. However, $P(c=0) = 0.000045$, using the Poisson formula. This is only 1/30 of the assumed area of 0.00135. So one has to raise the lower limit so as to get as close as possible to 0.00135. From Poisson tables or computer software we find that $P(1) = 0.0005$ and $P(2) = 0.0027$, so the lower limit should actually be 2 or 3.
Transforming count data into approximately normal data	To avoid this type of problem, we may resort to a transformation that makes the transformed data match the normal distribution better. One such transformation described by Ryan (2000) is $$ Y = 2 \sqrt{c} \, , $$ which is, for a large sample, approximately normally distributed with mean = 2$\sqrt{\lambda}$ and variace = 1, where $\lambda$ is the mean of the Poisson distribution. Similar transformations have been proposed by Anscombe (1948) and Freeman and Tukey (1950). When applied to a $c$ chart these are $$ y_1 = 2\sqrt{c + 3/8} $$ and $$ y_2 = \sqrt{c} + \sqrt{c+1} \, . $$ The respective control limits are $$ \bar{y} \pm 3, \,\,\, \bar{y}_{1} \pm 3, \,\, \mbox{ and } \,\,\, \bar{y}_{2} = \pm 3 \, .$$ While using transformations may result in meaningful control limits, one has to bear in mind that the user is now working with data on a different scale than the original measurements. There is another way to remedy the problem of symmetric limits applied to non symmetric cases, and that is to use probability limits. These can be obtained from tables given by Molina (1973). This allows the user to work with data on the original scale, but they require special tables to obtain the limits. Of course, software might be used instead.
Warning for highly skewed distributions	Note: In general, it is not a good idea to use 3-sigma limits for distributions that are highly skewed (see Ryan and Schwertman (1997) for more about the possibly extreme consequences of doing this).