5.
Process Improvement
5.5.
Advanced topics
5.5.4.
What is a mixture design?
5.5.4.2.
|
Simplex-lattice designs
|
|
Definition of simplex-
lattice points
|
A {q, m} simplex-lattice design for q components consists
of points defined by the following coordinate settings: the proportions
assumed by each component take the m+1 equally spaced values
from 0 to 1,
xi = 0, 1/m,
2/m, ... , 1 for i = 1, 2, ... , q
and all possible combinations (mixtures) of the proportions from
this equation are used.
|
|
Except for the center, all design points are on the simplex
boundaries
|
Note that the standard Simplex-Lattice and the Simplex-Centroid designs
(described later) are boundary-point designs; that is, with the
exception of the overall centroid, all the design points are on the
boundaries of the simplex. When one is interested in prediction
in the interior, it is highly desirable to augment the simplex-type
designs with interior design points.
|
Example of a three-
component simplex lattice design
|
Consider a three-component mixture for which the number of equally
spaced levels for each component is four (i.e., xi
= 0, 0.333, 0.667, 1). In this example q = 3 and m = 3.
If one uses all possible blends of the three components with these
proportions, the {3, 3} simplex-lattice then contains the 10 blending
coordinates listed in the table below. The experimental region and the
distribution of design runs over the simplex region are shown in the
figure below. There are 10 design runs for the {3, 3} simplex-lattice
design.
|
|
Design table
|
TABLE 5.3 Simplex Lattice Design
|
X1
|
X2
|
X3
|
|
|
0
|
0
|
1
|
|
0
|
0.333
|
0.667
|
|
0
|
0.667
|
0.333
|
|
0
|
1
|
0
|
|
0.333
|
0
|
0.667
|
|
0.333
|
0.333
|
0.333
|
|
0.333
|
0.6667
|
0
|
|
0.667
|
0
|
0.333
|
|
0.667
|
0.333
|
0
|
|
1
|
0
|
0
|
|
|
Diagram showing configuration of design runs
|
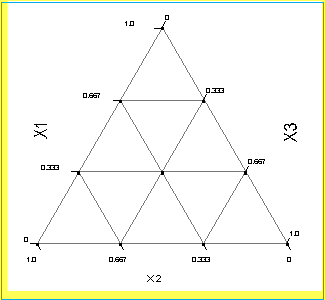
FIGURE 5.9 Configuration of Design Runs for a {3,3}
Simplex-Lattice Design
The number of design points in the simplex-lattice is
(q+m-1)!/(m!(q-1)!).
|
|
Definition of canonical polynomial model used in mixture
experiments
|
Now consider the form of the polynomial model that one might fit to
the data from a mixture experiment. Due to the restriction
x1 + x2 + ... + xq
= 1, the form of the regression function that is fit to the data from
a mixture experiment is somewhat different from the traditional
polynomial fit and is often referred to as the canonical polynomial.
Its form is derived using the general form of the regression function
that can be fit to data collected at the points of a
{q, m} simplex-lattice design and substituting into this
function the dependence relationship among the xi
terms. The number of terms in the {q, m} polynomial is
(q+m-1)!/(m!(q-1)!), as stated previously.
This is equal to the number of points that make up the associated
{q, m} simplex-lattice design.
|
Example for a {q, m=1} simplex-
lattice design
|
For example, the equation that can be fit to the points from a
{q, m=1} simplex-lattice design is
\( E(Y) = \beta_{0} + \beta_{1}x_{1} + \cdots + \beta_{q}x_{q} \)
Multiplying β0
by (x1 + x2 + ... +
xq = 1), the resulting equation is
\( E(Y) = \beta_{1}^{\star}x_{1} + \cdots + \beta_{q}^{\star}x_{q} \)
with \( \small \beta_{i}^{\star} = \beta_{0} + \beta_{i} \)
for all i = 1, ..., q.
|
First-
order canonical form
|
This is called the canonical form of the first-order mixture model.
In general, the canonical forms of the mixture models (with the
asterisks removed from the parameters) are as follows:
|
|
Summary of canonical mixture models
|
|
Linear
|
\[ E(Y) = \sum_{i=1}^{q}{\beta_{i}x_{i}} \]
|
|
Quadratic
|
\[ E(Y) = \sum_{i=1}^{q}{\beta_{i}x_{i}} +
\sum_{i=1}^{q}{\sum_{i < j}^{q}{\beta_{ij}x_{i}x_{j}}}
\]
|
|
Cubic
|
\[ \begin{array}{lcl}
E(Y) & = & \sum_{i=1}^{q}{\beta_{i}x_{i}} +
\sum_{i=1}^{q}{\sum_{i < j}^{q}{\beta_{ij}x_{i}x_{j}}}
+ \\
& & \sum_{i=1}^{q}{\sum_{i < j}^{q}
{\delta{ij}x_{i}x_{j}(x_{i} - x_{j})}}
+ \\
& & \sum_{k=1}^{q}{\sum_{j < k}^{q}{\sum_{i < j}^{q}
{\beta_{ijk}x_{i}x_{j}x_{k}}}}
\end{array}
\]
|
|
Special Cubic
|
\[ \begin{array}{lcl}
E(Y) & = & \sum_{i=1}^{q}{\beta_{i}x_{i}} +
\sum_{i=1}^{q}{\sum_{i < j}^{q}{\beta_{ij}x_{i}x_{j}}}
+ \\
& & \sum_{k=1}^{q}{\sum_{j < k}^{q}{\sum_{i < j}^{q}
{\beta_{ijk}x_{i}x_{j}x_{k}}}}
\end{array}
\]
|
|
|
Linear blending portion
|
The terms in the canonical mixture polynomials have simple
interpretations. Geometrically, the parameter βi
in the above equations represents the expected response to the pure
mixture xi=1, xj=0, i ≠ j,
and is the height of the mixture surface at the vertex
xi=1. The portion of each of the above polynomials
given by
\[ \sum_{i=1}^{q}{\beta_{i}x_{i}} \]
is called the linear blending portion. When blending is strictly
additive, then the linear model form above is an appropriate model.
|
Three-
component mixture example
|
The following example is from
Cornell (1990)
and consists of a
three-component mixture problem. The three components are Polyethylene
(X1), polystyrene (X2), and
polypropylene (X3), which are blended together to form
fiber that will be spun into yarn. The product developers are only
interested in the pure and binary blends of these three materials. The
response variable of interest is yarn elongation in kilograms of force
applied. A {3,2} simplex-lattice design is used to study the blending
process. The simplex region and the six design runs are shown in the
figure below. The design and the observed responses are listed in
Table 5.4. There were two replicate observations run at each of the pure
blends. There were three replicate observations run at the binary
blends. There are 15 observations with six unique design runs.
|
|
Diagram showing the designs runs for this example
|
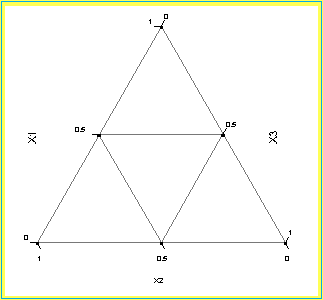
FIGURE 5.10 Design Runs for the {3,2} Simplex-Lattice Yarn
Elongation Problem
|
Table showing the simplex-
lattice design and observed responses
|
TABLE 5.4 Simplex-Lattice Design for Yarn Elongation
Problem
|
X1
|
X2
|
X3
|
Observed
Elongation Values
|
|
|
0.0
|
0.0
|
1.0
|
16.8, 16.0
|
|
0.0
|
0.5
|
0.5
|
10.0, 9.7, 11.8
|
|
0.0
|
1.0
|
0.0
|
8.8, 10.0
|
|
0.5
|
0.0
|
0.5
|
17.7, 16.4, 16.6
|
|
0.5
|
0.5
|
0.0
|
15.0, 14.8, 16.1
|
|
1.0
|
0.0
|
0.0
|
11.0, 12.4
|
|
|
Fit a quadratic mixture model
|
The design runs listed in the above table are in standard order. The
actual order of the 15 treatment runs was completely randomized.
Since there are three
levels of each of the three mixture components, a quadratic mixture
model can be fit to the data. The results of the model fit are shown
below. Note that there was no intercept in the model.
Summary of Fit
RSquare 0.951356
RSquare Adj 0.924331
Root Mean Square Error 0.85375
Mean of Response 13.54
Observations (or Sum Wgts) 15
Analysis of Variance
Source DF Sum of Squares Mean Square F Ratio Prob > F
Model 5 2878.27 479.7117 658.141 1.55e-13
Error 9 6.56 0.7289
C Total 14 2884.83
Parameter Estimates
Term Estimate Std Error t Ratio Prob>|t|
X1 11.7 0.603692 19.38 <.0001
X2 9.4 0.603692 15.57 <.0001
X3 16.4 0.603692 27.17 <.0001
X2*X1 19 2.608249 7.28 <.0001
X3*X1 11.4 2.608249 4.37 0.0018
X3*X2 -9.6 2.608249 -3.68 0.0051
|
|
Interpretation of results
|
Under the parameter estimates section of the output are the individual
t-tests for each of the parameters in the model. The three cross
product terms are significant (X1*X2,
X3*X1,
X3*X2), indicating a significant
quadratic fit.
|
|
The fitted quadratic model
|
The fitted quadratic mixture model is
\( \small \hat{y} = 11.7 x_{1} + 9.4 x_{2} + 16.4 x_{3} + 19.0 x_{1} x_{2}
+ 11.4 x_{1} x_{3} - 9.6 x_{2} x_{3} \)
|
|
Conclusions from the fitted quadratic model
|
Since b3 > b1 > b2, one can conclude
that component 3 (polypropylene) produces yarn with the highest
elongation. Additionally, since b12 and b13
are positive, blending components 1 and 2 or components 1 and 3
produces higher elongation values than would be expected just by
averaging the elongations of the pure blends. This is an example of
'synergistic' blending effects. Components 2 and 3 have antagonistic
blending effects because b23 is negative.
|
|
Contour plot of the predicted elongation values
|
The figure below is the contour plot of the elongation values. From
the plot it can be seen that if maximum elongation is desired, a blend
of components 1 and 3 should be chosen consisting of about 75% - 80%
component 3 and 20% - 25% component 1.
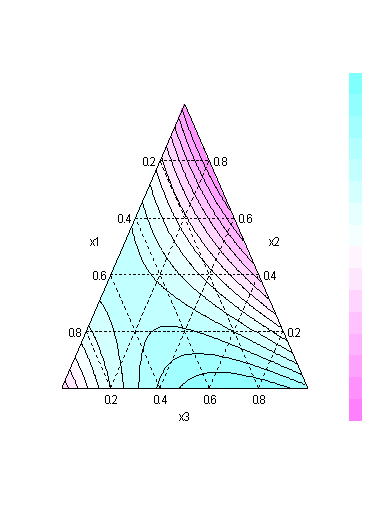
FIGURE 5.11 Contour Plot of Predicted Elongation Values from
{3,2} Simplex-Lattice Design
The analyses in this page can be obtained using
R code.
|




