5.
Process Improvement
5.5.
Advanced topics
5.5.4.
What is a mixture design?
5.5.4.4.
|
Constrained mixture designs
|
|
|
Upper and/or lower bound constraints may be present
|
In mixture designs when there are constraints on the component
proportions, these are often upper and/or lower bound constraints
of the form
Li ≤ xi ≤
Ui, i = 1, 2,..., q, where
Li is the lower bound for the i-th component
and Ui the upper bound for the i-th
component. The general form of the constrained mixture problem is
|
|
Typical additional constraints
|
x1 + x2 + ... +
xq = 1
Li  xi
xi  Ui, for i = 1, 2,..., q
Ui, for i = 1, 2,..., q
with Li ≥ 0 and Ui ≤ 1.
|
|
Example using only lower bounds
|
Consider the following case in which only the lower bounds in the
above equation are imposed, so that the constrained mixture problem
becomes
x1 + x2 + ... +
xq = 1
Li ≤ xi ≤ 1,
for i = 1, 2,..., q
Assume we have a three-component mixture problem with constraints
0.3 ≤ x1
0.4 ≤ x2
0.1 ≤ x3
|
|
Feasible mixture region
|
The feasible mixture space is shown in the figure below. Note that
the existence of lower bounds does not affect the shape of the mixture
region, it is still a simplex region. In general, this will always be
the case if only lower bounds are imposed on any of the component
proportions.
|
|
Diagram showing the feasible mixture space
|
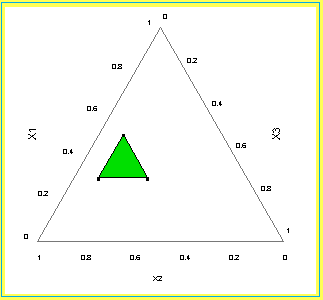
FIGURE 5.12: The Feasible Mixture Space (Shaded Region) for
Three Components with Lower Bounds
|
|
A simple transformation helps in design construction and analysis
|
Since the new region of the experiment is still a simplex, it is
possible to define a new set of components that take on the values
from 0 to 1 over the feasible region. This will make the design
construction and the model fitting easier over the constrained
region of interest. These new components
( )
are called pseudo components and are defined using the following
formula
|
|
Formula for pseudo components
|
with
denoting the sum of all the lower bounds.
|
|
Computation of the pseudo components for the example
|
In the three component example above, the pseudo components are
|
|
|
|
Constructing the design in the pseudo components
|
Constructing a design in the pseudo components is accomplished by
specifying the design points in terms of the
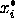 and then converting them to the original component settings using
and then converting them to the original component settings using
|
|
Select appropriate design
|
In terms of the pseudo components, the experimenter has the choice
of selecting a Simplex-Lattice or a Simplex-Centroid design, depending
on the objectives of the experiment.
|
|
Simplex-centroid design example (after transformation)
|
Suppose, we decided to use a Simplex-centroid design for the
three-component experiment. The table below shows the design points
in the pseudo components, along with the corresponding setting for
the original components.
|
|
Table showing the design points in both the pseudo components and
the original components
|
TABLE 5.5:
Pseudo Component Settings and Original Component Settings,
Three-Component Simplex-Centroid Design
|
Pseudo Components
|
|
Original Components
|
|
X1
|
X2
|
X3
|
|
|
|
|
|
|
1
|
0
|
0
|
|
0.5
|
0.4
|
0.1
|
|
0
|
1
|
0
|
|
0.3
|
0.6
|
0.1
|
|
0
|
0
|
1
|
|
0.3
|
0.4
|
0.3
|
|
0.5
|
0.5
|
0
|
|
0.4
|
0.5
|
0.1
|
|
0.5
|
0
|
0.5
|
|
0.4
|
0.4
|
0.2
|
|
0
|
0.5
|
0.5
|
|
0.3
|
0.5
|
0.2
|
|
0.3333
|
0.3333
|
0.3333
|
|
0.3667
|
0.4667
|
0.1666
|
|
|
Use of pseudo components (after transformation) is recommended
|
It is recommended that the pseudo components be used to fit the
mixture model. This is due to the fact that the constrained design
space will usually have relatively high levels of multicollinearity
among the predictors. Once the final predictive model for the pseudo
components has been determined, the equation in terms of the original
components can be determined by substituting the relationship between
xi and .
|
|
D-optimal designs can also be used
|
Computer-aided designs (D-optimal,
for example) can be used to select points for a mixture design in a
constrained region. See
Myers and Montgomery (1995)
for more details on using D-optimal designs in mixture experiments.
|
|
Extreme vertice designs are another option
|
Note: There are other mixture designs that cover only a
sub-portion or smaller space within the simplex. These types of
mixture designs (not covered here) are referred to as extreme
vertices designs. (See chapter 11 of
Myers and Montgomery (1995)
or
Cornell (1990).
|
 xi
xi  Ui, for i = 1, 2,..., q
Ui, for i = 1, 2,..., q

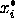 and then converting them to the original component settings using
and then converting them to the original component settings using

