5.
Process Improvement
5.5.
Advanced topics
5.5.9.
An EDA approach to experimental design
5.5.9.9.
Cumulative residual standard deviation plot
5.5.9.9.7.
|
Motivation: How do we use the Model to Generate
Predicted Values?
|
|
|
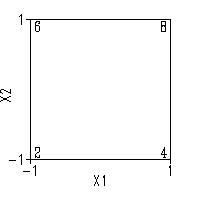
Design matrix with response for two factors
|
To illustrate the details as to how a model may be used for prediction,
let us consider a simple case and generalize from it. Consider the
simple Yates-order 22 full factorial design in X1
and X2, augmented with a response vector Y:
|
X1
|
X2
|
Y
|
|
-
|
-
|
2
|
|
+
|
-
|
4
|
|
-
|
+
|
6
|
|
+
|
+
|
8
|
|
|
Geometric representation
|
This can be represented geometrically
|
|
Determining the prediction equation
|
For this case, we might consider the model
\( Y = c + B_{1}X_{1} + B_{2}X_{2} + B_{12}X_{1}X_{2} + \epsilon \)
From the above diagram, we may deduce that the estimated factor
effects are:
|
c
|
=
=
|
the average response = \( \bar{Y} \)
(2 + 4 + 6 + 8) / 4 = 5
|
|
E1
|
=
=
|
average change in Y as X1 goes from -1 to +1
((4-2) + (8-6)) / 2 = (2 + 2) / 2 = 2
Note: the (4-2) is the change in Y (due to
X1) on the lower axis; the (8-6) is the change in
Y (due to X1) on the upper axis.
|
|
E2
|
=
=
|
average change in Y as X2 goes from -1 to +1
((6-2) + (8-4)) / 2 = (4 + 4) / 2 = 4
|
|
E12
|
=
=
|
interaction = (the less obvious) average change in Y as
X1*X2 goes from -1 to +1
((2-4) + (8-6)) / 2 = (-2 + 2) / 2 = 0
|
For factors coded using +1 and -1, the least-squares estimate of a
coefficient is one half of the effect estimate (Bi =
Ei / 2), so the fitted model (that is, the prediction
equation) is
\( \hat{Y} = 5 + 1 X_{1} + 2 X_{2} + 0 X_{1} X_{2} \)
or with the terms rearranged in descending order of importance
\( \hat{Y} = 5 + 2 X_{2} + X_{1} \)
|
|
Table of fitted values
|
Substituting the values for the four design points into this
equation yields the following fitted values
|
X1
|
X2
|
Y
|
\( \scriptsize \hat{Y} \)
|
|
-
|
-
|
2
|
2
|
|
+
|
-
|
4
|
4
|
|
-
|
+
|
6
|
6
|
|
+
|
+
|
8
|
8
|
|
|
Perfect fit
|
This is a perfect-fit model. Such perfect-fit models will result
anytime (in this orthogonal 2-level design family) we include all main
effects and all interactions. Remarkably, this is true not only for
k = 2 factors, but for general k.
|
|
Residuals
|
For a given model (any model), the difference between the
response value Y and the predicted value \( \hat{Y} \)
is referred to as the "residual":
residual = Y - \( \small \hat{Y} \)
The perfect-fit full-blown (all main factors and all interactions of all
orders) models will have all residuals identically zero.
The perfect fit is a mathematical property that comes if we choose to
use the linear model with all possible terms.
|
|
Price for perfect fit
|
What price is paid for this perfect fit? One price is that the variance
of \( \scriptsize \hat{Y} \)
is increased unnecessarily. In addition, we have a non-parsimonious
model. We must compute and carry the average and the coefficients of
all main effects and all interactions. Including the average, there
will in general be 2k coefficients
to fully describe the fitting of the n = 2k
points. This is very much akin to the Y = f(X)
polynomial fitting of n distinct points. It is well known that
this may be done "perfectly" by fitting a polynomial of degree
n-1. It is comforting to know that such perfection is
mathematically attainable, but in practice do we want to do this all
the time or even anytime? The answer is generally "no" for two reasons:
- Noise: It is very common that the response data Y has
noise (= error) in it. Do we want to go out of our way to fit
such noise? Or do we want our model to filter out the noise and
just fit the "signal"? For the latter, fewer coefficients may
be in order, in the same spirit that we may forego a
perfect-fitting (but jagged) 11-th degree polynomial to 12 data
points, and opt out instead for an imperfect (but smoother) 3rd
degree polynomial fit to the 12 points.
- Parsimony: For full factorial designs, to fit the n =
2k points we would need to compute
2k coefficients. We gain information by noting
the magnitude and sign of such coefficients, but numerically we
have n data values Y as input and n
coefficients B as output, and so no numerical reduction
has been achieved. We have simply used one set of n
numbers (the data) to obtain another set of n numbers (the
coefficients). Not all of these coefficients will be equally
important. At times that importance becomes clouded by the sheer
volume of the n = 2k coefficients.
Parsimony suggests that our result should be simpler and
more focused than our n starting points. Hence fewer
retained coefficients are called for.
The net result is that in practice we almost always give up the
perfect, but unwieldy, model for an imperfect, but parsimonious,
model.
|
|
Imperfect fit
|
The above calculations illustrated the computation of predicted values
for the full model. On the other hand, as discussed above, it will
generally be convenient for signal or parsimony purposes to deliberately
omit some unimportant factors. When the analyst chooses such a model,
we note that the methodology for computing predicted values
\( \scriptsize \hat{Y} \)
is precisely the same. In such a case, however, the resulting predicted
values will in general not be identical to the original response
values Y; that is, we no longer obtain a perfect fit. Thus, linear
models that omit some terms will have virtually all non-zero residuals.
|