SED navigation bar go to SED home page go to Dataplot home page go to NIST home page SED Home Page SED Staff SED Projects SED Products and Publications Search SED Pages
Dataplot Vol 1 Vol 2

POISSON PLOT

Name:
    POISSON PLOT
Type:
    Graphics Command
Purpose:
    Generates one of the following types of plots:

    1. a Poisson plot
    2. a geometric plot
    3. a negative binomial plot
    4. a binomial plot
    5. a logarithmic series plot
Description:
    These plots are used to determine if the specified distribution provides an appropriate distributiuonal model to a set of data. These are similar in concept to probability plots in that we generate a plot that should appear linear if the data are in fact fit well by the distribution.

    The following table shows how these plots are constructed where x and nx denote the class value and the corresponding frequency. In all cases, the x-coordinate is x.

    Distribution \( \phi (n_{x}^{*}) \)
    Y-Axis
    Coordinate     		Theoretical
    Slope     		Theoretical
    Intercept
    Poisson \( \log \left( \frac{x!n_{x}^{*}}{N} \right) \) \( \log(\lambda) \) \( -\lambda \)
    Geometric \( \log \left( \frac{n_{x}^{*}}{N} \right) \) log(1-p) log(p)
    Negative Binomial \( \log ( \frac{n_{x}^{*}} {N \left( \begin{array}{c} n+x-1 \\ x \end{array} \right) } ) \) log(1-p) n log(p)
    Binomial \( \log ( \frac{n_{x}^{*}} {N \left( \begin{array}{c} n \\ x \end{array} \right) } ) \) log(p/(1-p)) n log(1-p)
    Logarithmic Series \( \log \left( \frac{x n_{x}^{*}}{N} \right) \) \( \log(\theta) \) \( -\log(-\log(1 - \theta)) \)

where

    p = probability of success parameter for the geometric, binomial, and negative binomial distributions.
    \( \theta \) = the shape parameter for the logarithmic series distribution.
    n = the number of trials parameter for the binomial distribution.

The theoretical slope parameter can be used to estimate the shape parameter of the distribution.

Hoaglin and Tukey (see References below) provides the derivations of why these plots should be linear if the specified distribution is appropriate. They also make the following suggestions for enhancing these plots:

  1. A 95% confidence interval for each point on the plot is given as

      \( \phi (n_{x}^{*}) \pm h(x) \)

    where

      \( n_{x}^{*} \) = nx - 0.8 nx/N - 0.67 nx ≥ 2
        = 1/e nx = 1
        = undefined nx = 0
      h(x) = \( \frac{1.96 \sqrt{1 - \hat{p_{x}}}} {\sqrt{n_{x} - (0.25 \hat{p_{x}} + 0.47) \sqrt{n_{x}}}} \)  
      N = total sample size  
      \( \hat{p_{x}} \) = \( \frac{n_{x}} {N} \)  

    The rationale for this confidence interval is given in the Hoaglin and Tukey reference.

    The \( n_{x}^{*} \) values are referred to as the adjusted frequencies.

  2. These plots can be "leveled". By leveling, we convert the plot from interpretation of departures from a diagonal line to departures from a horizontal line. This may be an easier visual task.

    To level the plot, we plot

      \( \phi^{'} (n_{x}) \) = \( \phi (n_{x}) \) - (intercept + slope*x)

    where intercept and slope are taken from the columns "theoretical intercept" and "theoretical slope" in the table above.

    Note that a preliminary estimate of the shape parameter for the distribution is required to compute the theoretical intercept and the theoretical slope. This is discussed further in a Note section below.

Syntax 1:
    <dist> PLOT <y>             <SUBSET/EXCEPT/FOR qualification>
    where <y> is a response variable;
                <dist> is one of the following:
      POISSON
      GEOMETRIC
      NEGATIVE BINOMIAL
      BINOMIAL
      LOGARITHMIC SERIES;
    and where the <SUBSET/EXCEPT/FOR qualification> is optional.

    This syntax is used for the case where you have raw data. Dataplot will automatically create the frequency table.

Syntax 2:
    <dist> PLOT <y> <x>             <SUBSET/EXCEPT/FOR qualification>
    where <y> is a variable containing frequencies;
                <x> is a variable containing the class value;
                <dist> is one of the disributions listed above;
    and where the <SUBSET/EXCEPT/FOR qualification> is optional.

    This syntax is used for the case where your data is in the form of a frequency table.

Examples:
    POISSON PLOT Y
    POISSON PLOT Y X
    GEOMETRIC PLOT Y
    GEOMETRIC PLOT Y X
Note:
    For the leveled version of the plot, a preliminary estimate of the shape parameter(s) is required.

    1. For the Poisson distribution, the maximum likelihood estimate of \( \lambda \) is the sample mean. This is used as the prelimanary estimate of \( \lambda \) in the leveled version of the plot.

    2. For the binomial distribution, you need to specify the n parameter (the number of trials) by entering the following command before the BINOMIAL PLOT command:

        LET N = <value>

      The sample mean is then used as the estimate of the p (probability of success) parameter. This is the maximum likelihood estimate.

    3. For the geometric distribution, the maximum likelihood estimate of the p (probability of success) parameter is

        \( \frac{1} {\bar{x} + 1} \)

      where \( \bar{x} \) is the sample mean.

    4. For the negative binomial distribution, there are two parameters: p and k. For this plot, k is restricted to integer values.

      You can either specify a value for k by entering the command

      LET K = <value>

      or you can let Dataplot estimate the value.

      If k is not specified, the moment estimate of k is used:

        \( \hat{k} = \frac{\hat{x}^2}{s^2 - \bar{x}} \)

      This estimate will be rounded to the nearest integer.

      The maximum likelihood estimate of p is then

        \( \hat{p} = \frac{k} {\bar{x} + k} \)

      If k ≥ 2, then the bias corrected estimate is used

        \( \hat{p} = \frac{k-1} {\bar{x} + k - 1} \)

    5. For the logarithmic series distribution, you can specify the desired value of theta by entering the command

        LET THETA = <value>

      You can obtain this estimate either by using maximum likelihood, the PPCC plot, or the KS plot.

Note:
    The appearance of the plot can be controlled with the LINE and CHARACTER commands. Specifically,

      trace 1 = \( \phi(n_x) \) versus x
      trace 2 = fitted line for \( \phi(n_x) \) versus x
      trace 3 = \( \phi (n_{x}^{*}) \) versus x
      trace 4 = fitted line for \( \phi (n_{x}^{*}) \) versus x
      trace 5 = lower confidence point
      trace 6 = upper confidence point
      trace 7 and above = line connecting the lower and upper confidence points

    If you want to suppress any of these components, you can set both the CHARACTER and LINE settings to BLANK. The example programs below demonstrate the use of the LINE and CHARACTER commands to control the appearance of the plot.

Note:
    By default, the unleveled plot is generated. To generate the leveled plot, enter the command

      SET POISSON PLOT LEVEL ON

    To reset the default, enter the command

      SET POISSON PLOT LEVEL OFF

    This command applies to all five of the plots described here, not just the Poisson plot.

Note:
    The following internal parameters are saved by this plot:

    All plots:

      PPA0 = the intercept of the fitted line (unadjusted frequencies)
      PPA1 = the slope of the fitted line (unadjusted frequencies)
      PPA0ADJU = the intercept of the fitted line (adjusted frequencies)
      PPA1 = the slope of the fitted line (adjusted frequencies)

    Poisson plot:

      LAMBDAPP = the estimate of \( \lambda \) based on the unadjusted frequencies
      LAMBDAPA = the estimate of \( \lambda \) based on the adjusted frequencies

    Binomial, negative binomial, geometric plot:

      PPP = the estimate of p based on the unadjusted frequencies
      PPPADJ = the estimate of p based on the adjusted frequencies
    Logarithmic series plot:

      THETAPP = the estimate of \( \theta \) based on the unadjusted frequencies
      THETAPPA = the estimate of \( \theta \) based on the adjusted frequencies
Default:
    The unleveled version of the plot is generated by default.
Synonyms:
    None
Related Commands: References:
    Hoaglin (1980), "A Poissonness Plot", The American Statistician, 34, pp. 146-149.

    Hoaglin and Tukey (1985), "Checking The Shape of Discrete Distributions". In Hoaglin, Mosteller, and Tukey, editors, "Exploring Data Tables, Trends, and Shapes", chapter 9, John Wiley and Sons, New York.

    Friendly (2000), "Visualizing Categorical Data", SAS Publishing, Cary, NC, pp. 49-56.

Applications:
    Distributional Modeling
Implementation Date:
    2007/5
Program: 
     
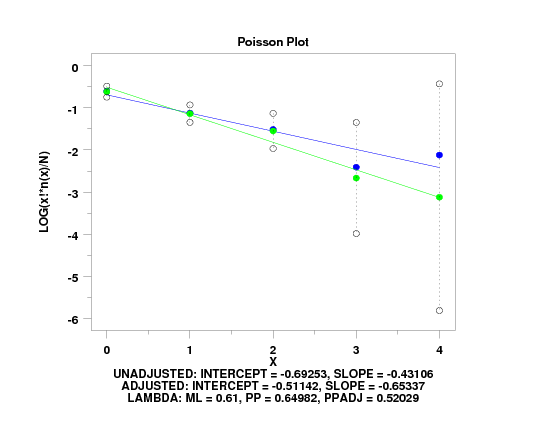
.  Following data from p. 51 of Friendly
read x y
0  109
1   65
2   22
3    3
4    1
end of data
.
title case asis
title offset 2
label case asis
x1label displacement 6
title Poisson Plot
x1label X
y1label LOG(x!*n(x)/N)
x3label
.
char blank all
char fill off all
char hw 1.5 1.2 all
char color black all
char circle blank circle blank circle circle
char fill on off on
char color blue black green
line dotted all
line blank solid blank solid blank blank
line color black blue black green
tic offset units screen
tic offset 3 3
.
poisson plot y x
.
let lambml = weighted mean x y
justification center
move 50 8
text Unadjusted: Intercept = ^ppa0, Slope = ^ppa1
move 50 5
text Adjusted: Intercept = ^ppa0adju, Slope = ^ppa1adju
move 50 2
text Lambda: ML = ^lambml, PP = ^lambdapp, PPadj = ^lambdapa
    plot generated by sample program

Date created: 07/25/2007
Last updated: 12/04/2023
Please email comments on this WWW page to alan.heckert@nist.gov.