QUANTILE QUANTILE PLOT

QUANTILE-QUANTILE PLOT

Graphics Command

Generates a quantile-quantile plot.

A quantile-quantile plot (or q-q plot) is a graphical data analysis technique for comparing the distributions of 2 data sets. The quantile-quantile plot is a graphical alternative for the various classical 2-sample tests (e.g., t for location, F for dispersion). The plot consists of the following:

Vertical axis	=	estimated quantiles from data set 1;
Horizontal axis	=	estimated quantiles from data set 2.

The "quantiles" of a distribution are the distribution's "percent points" (e.g., .5 quantile = 50% point = median). The advantage of the quantile-quantile plot is 2-fold:

1. the sample sizes do not need to be identical;
2. many distributional aspects can be simultaneously tested. For example, shifts in location, shifts in dispersion, changes in symmetry/skewness, outliers, etc.

The quantile-quantile plot has 3 components:

1. the quantile points themselves;
2. a 45 degree reference line;
3. a least squares line fit to the quantile points.

If the two data sets come from similar distributions, then the points of the q-q plot should lie along the 45 degree reference line.

Like usual, the appearance of these 2 components is controlled by the first 2 settings of the CHARACTERS and LINES commands. It is typical for the quantile points to be represented as, say, X's with no connecting line, and the reference line to have no plot characters but to be solid. This is demonstrated in the sample programs below.

QUANTILE-QUANTILE PLOT <y1> <y2>
                        <SUBSET/EXCEPT/FOR qualification>
where <y1> is the first response variable;
            <y2> is the second response variable;
and where the <SUBSET/EXCEPT/FOR qualification> is optional.

HIGHLIGHT QUANTILE-QUANTILE PLOT <y1> <y2> <tag>
                        <SUBSET/EXCEPT/FOR qualification>
where <y1> is the first response variable;
            <y2> is the second response variable;
            <tag> is a group-id variable that defines the highlighting;
and where the <SUBSET/EXCEPT/FOR qualification> is optional.

This syntax can be used to plot different plot points with different attributes. For example, it can used to highlight groups in the data or to emphasize the extremes.

QUANTILE-QUANTILE PLOT Y1 Y2
QUANTILE-QUANTILE PLOT RUN1 RUN2
QUANTILE-QUANTILE PLOT BATCH1 BATCH2
QUANTILE-QUANTILE PLOT Y1 Y2 SUBSET AUTO 4
QUANTILE-QUANTILE PLOT Y1 Y2 SUBSET STATE 25

One of the distributions can be a theoretical distribution. For example, the following program generates a quantile-quantile plot of a data set against a normal distribution (this is called a normal quantile plot).
LET Y1 = NORMAL RANDOM NUMBERS FOR I = 1 1 100
LET X = SEQUENCE .01 .01 .99
LET Y2 = NORPPF(X)
QUANTILE-QUANTILE PLOT Y1 Y2


This same technique can be used other distributions (use the proper PPF function). This is also fairly close to what a probability plot does (DATAPLOT has a PROBABILITY PLOT command for over 25 distributions).

For large data sets, it may be impractical to generate the plot for each individual point. As an alternative, you can generate the plot for a user specified number of quantiles. To do this, enter the command
SET QUANTILE QUANTILE PLOT NUMBER OF PERCENTILES ...
            <value>


where <value> specifies the desired number of quantiles. This is demonstrated in the Program 2 example below.

If the two data sets have similar distribution, then the points on the plot should fall along the 45 degree reference line. For example, if you enter a QUANTILE QUANTILE PLOT Y Y command, then the points will lie exactly on the reference line. This means that if a line is fit to the points on the plot and the two data sets come from similar distributions, then the itercept and the slope of the fitted line should be close to zero and one, respectively. In addition, the correlation coefficient of the fitted line should be close to one.

The parameters containing the intercept, slope, and correlation coefficient are automatically saved in the parameters PPA0, PPA1, and PPCC, respectively. This can be useful in labeling q-q plots.

If you have more than two data sets, you can generate a matrix plot of the pairwise q-q plots with the SCATTER PLOT MATRIX command. This is demonstrated in the Program 3 example.

None

None

TUKEY MEAN DIFFERENCE PLOT	=	Generates a Tukey mean difference plot.
MULTIPLOT	=	Allows multiple plots per page.
BOX PLOT	=	Generates a box plot.
BIHISTOGRAM	=	Generates a bihistogram.
PLOT	=	Generates a data or function plot.
PROBABILITY PLOT	=	Generates a probability plot.
T-TEST	=	Carries out a 2-sample t test.
F-TEST	=	Carries out a 2-sample F test.
ANOVA	=	Carries out an ANOVA.
CHARACTERS	=	Sets the type for plot characters.
LINES	=	Sets the type for plot lines.

Chambers, Cleveland, Kleiner, and Tukey (1983), "Graphical Methods of Data Analysis", Wadsworth, pp. 48-57.

Exploratory Data Analysis

1988/03
2011/02: Support for highlight option
2016/06: Support for SET QUANTILE QUANTILE PLOT NUMBER OF PERCENTILES
2016/06: Generate a fitted line to the quantile points
2016/06: Automatically save PPA0, PPA1, and PPCC

 
SKIP 25
READ AUTO83B.DAT Y1 Y2
DELETE Y2 SUBSET Y2 < 0
.
LINE BLANK SOLID DASHED
CHARACTER CIRCLE BLANK BLANK
CHARACTER FILL ON OFF OFF
CHARACTER HW 0.5 0.375
TITLE AUTOMATIC
TITLE OFFSET 2
LABEL CASE ASIS
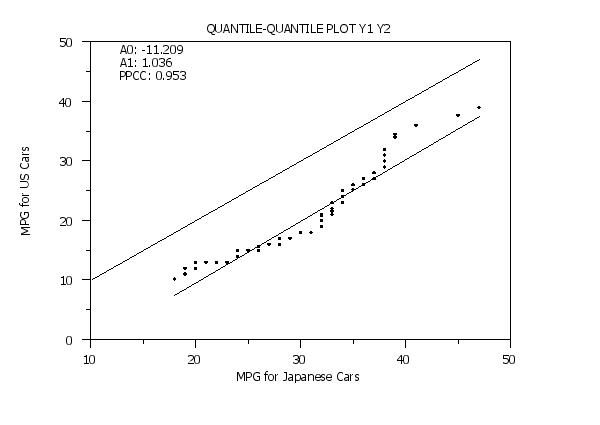
Y1LABEL MPG for US Cars
X1LABEL MPG for Japanese Cars
.
QUANTILE-QUANTILE PLOT Y1 Y2
.
LET PPA0 = ROUND(PPA0,3)
LET PPA1 = ROUND(PPA1,3)
LET PPCC = ROUND(PPCC,3)
JUSTIFICATION LEFT
MOVE 20 87; TEXT A0: ^PPA0
MOVE 20 85; TEXT A1: ^PPA1
MOVE 20 83; TEXT PPCC: ^PPCC
    

 
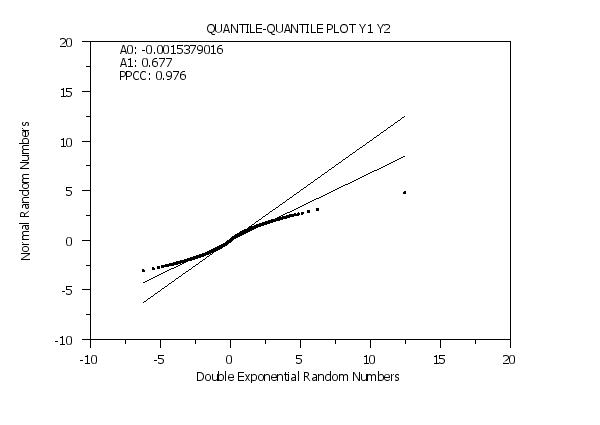
LET Y1 = NORMAL RANDOM NUMBER FOR I = 1 1 1000000
LET Y2 = DOUBLE EXPONENTIAL RANDOM NUMBER FOR I = 1 1 1000000
.
LINE BLANK SOLID DASH
CHARACTER CIRCLE BLANK BLANK
CHARACTER FILL ON OFF
CHARACTER HW 0.5 0.375
TITLE AUTOMATIC
TITLE OFFSET 2
LABEL CASE ASIS
Y1LABEL Normal Random Numbers
X1LABEL Double Exponential Random Numbers
.
SET QUANTILE QUANTILE PLOT NUMBER OF PERCENTILES 1000
QUANTILE-QUANTILE PLOT Y1 Y2
.
LET PPA0 = ROUND(PPA),3)
LET PPA1 = ROUND(PPA1,3)
LET PPCC = ROUND(PPCC,3)
JUSTIFICATION LEFT
MOVE 20 87; TEXT A0: ^PPA0
MOVE 20 85; TEXT A1: ^PPA1
MOVE 20 83; TEXT PPCC: ^PPCC
    

 
SKIP 25
READ AUTO83B.DAT Y1 Y2
DELETE Y2 SUBSET Y2 < 0
.
LINE BLANK BLANK SOLID DASH
CHARACTER CIRCLE CIRCLE BLANK BLANK
CHARACTER FILL ON ON
CHARACTER HW 0.5 0.375 ALL
CHARACTER COLOR BLACK RED
TITLE AUTOMATIC
TITLE OFFSET 2
.
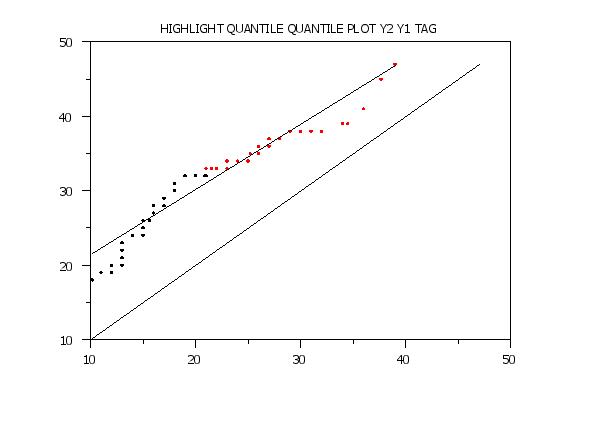
LET N2 = SIZE Y2
LET TAG = 1 FOR I = 1 1 N2
LET TAG = 2 SUBSET Y2 > 32
.
HIGHLIGHT QUANTILE QUANTILE PLOT Y2 Y1 TAG
    

. Step 1:   Read the data
.
skip 25
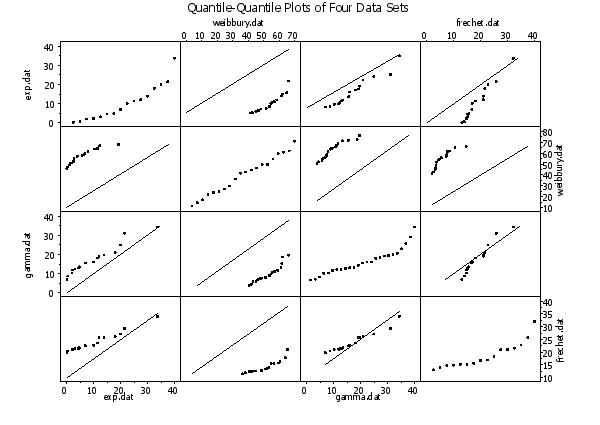
read exp.dat      y1
read weibbury.dat y2
read gamma.dat    y3
read frechet.dat  y4
skip 0
.
variable label y1 exp.dat
variable label y2 weibbury.dat
variable label y3 gamma.dat
variable label y4 frechet.dat
.
. Step 2:   Set some plot control features
.
case asis
label case asis
title case asis
title offset 2
tic mark offset units screen
tic mark offset 5 5
multiplot scale factor 4
multiplot corner coordinates 10 10 90 90
.
line blank solid blank blank
character circle blank blank blank
character fill on
character hw 0.5 0.375 all
.
. Step 3:   Scatter plot matrix of quantile-quantile plot
.
label displacement 18
set scatter plot matrix type quantile quantile
scatter plot matrix y1 y2 y3 y4
.
justification center
move 50 97
text Quantile-Quantile Plots of Four Data Sets