

|
BIWEIGHT MIDCORRELATIONName:
Many statistics have one of these properties. However, it can be difficult to find statistics that are both resistant and have robustness of efficiency. The standard Pearson correlation coefficient is the optimal estimator for Gaussian data. However, it is not resistant and it does not have robustness of efficiency. The Spearman rank correlation is one example of a robust estimate of correlation. The biweight midcorrelation estimator is another alternative correlation estimate. It is both resistant and robust of efficiency. The biweight midcorrelation can be defined in terms of the biweight midvariance and the biweight midcovariance:
where \( s_{bxy} \) is the biweight midcovariance between X and Y and \( s_{bxx} \) and \( s_{byy} \) are the biweight midvariances of X and Y, respectively.
<SUBSET/EXCEPT/FOR qualification> where <y1> is the first response variable; <y2> is the second response variable; <par> is a parameter where the computed biweight midcorrelation is stored; and where the <SUBSET/EXCEPT/FOR qualification> is optional.
LET A = BIWEIGHT MIDCORRELATION Y1 Y2 SUBSET TAG > 2
can be used to specify an alternate correlation measure to compute in the CORRELATION MATRIX command. The following types are supported:
Mosteller and Tukey (1977), "Data Analysis and Regression: A Second Course in Statistics," Addison-Wesley, pp. 203-209.
SKIP 25
READ MATRIX IRIS.DAT Y1 Y2 Y3 Y4 X
LET M = CREATE MATRIX Y1 Y2 Y3 Y4
SET CORRELATION TYPE BIWEIGHT
LET B = CORRELATION MATRIX Y1 Y2 Y3 Y4
Program 2:
SKIP 25
READ IRIS.DAT Y1 Y2 Y3 Y4 X
.
MULTIPLOT CORNER COORDINATES 0 0 100 95
MULTIPLOT 2 1
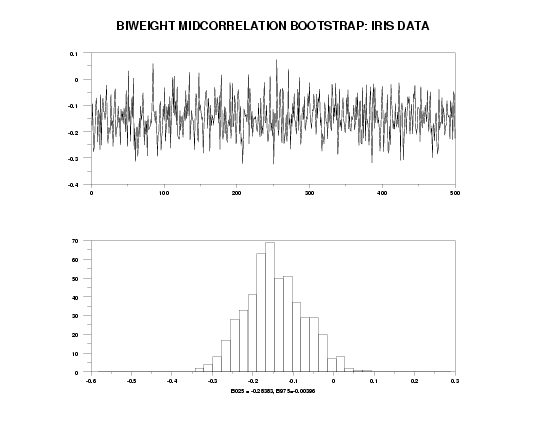
BOOTSTRAP SAMPLES 500
BOOTSTRAP BIWEIGHT MIDCORRELATION PLOT Y1 Y2
X1LABEL B025 = ^B025, B975=^B975
HISTOGRAM YPLOT
END OF MULTIPLOT
MOVE 50 96
JUSTIFICATION CENTER
TEXT BIWEIGHT MIDCORRELATION BOOTSTRAP: IRIS DATA
|
Privacy
Policy/Security Notice
NIST is an agency of the U.S.
Commerce Department.
Date created: 07/22/2002 | ||||||||||||||||||||||||||||||||