H15

H15 (LET)

Let Subcommand

Compute the H15 robust location or scale estimate of a variable.

The H15 location and scale estimates are computed as follows.

Let X = x₁, x₂, ..., x_p denote the response values and x* and s* denote the robust estimates of location and scale, respectively. The initial estimate for x* is the median. The initial estimate for s* is

s* = MAD(X)/0.6745

where MAD is the median absolute deviation.

To update the values for x* and s*, calculate

\( \delta \) = c s*

\( \begin{array}{lcll} x_{i}^{*} & = & x^{*} - \delta \hspace{10pt} & \mbox{if } x_{i} < x^{*} - \delta \\ & = & x^{*} + \delta \hspace{10pt} & \mbox{if } x_{i} > x^{*} + \delta \\ & = & x_{i} \hspace{10pt} & \mbox{otherwise} \end{array} \)

The updated values of x* and s* are

\( x^{*} = \frac{\sum_{i=1}^{p}{x_{i}}} {p} \)

\( s^{*} = \frac{1} {\beta^2} \sqrt{\frac{\sum_{i=1}^{p}{(x_i^{*} - x^{*})^2}} {p - 1}} \)

This process is iterated until the values of x* and s* converge.

For H15, c = 1.5 and \( \beta \) = 0.778. There are several alternative estimates that use different values for c and \( \beta \). Specifically,

• H10: c= 1.0 and \( \beta \) = 0.516
• H12: c= 1.1 and \( \beta \) = 0.578
• H12: c= 1.2 and \( \beta \) = 0.635
• H13: c= 1.3 and \( \beta \) = 0.688
• H14: c= 1.4 and \( \beta \) = 0.736
• H16: c= 1.6 and \( \beta \) = 0.816
• H17: c= 1.7 and \( \beta \) = 0.849
• H18: c= 1.8 and \( \beta \) = 0.877
• H19: c= 1.9 and \( \beta \) = 0.900
• H20: c= 2.0 and \( \beta \) = 0.921

Dataplot currently supports the H10, H12, H15, H17, H20 variations of this command. The H15 variant is the most commonly used.

In the ISO 5725-5 and ISO 13528 standards, H15 is referred to as "Algorithm A".

LET <par> = <stat> LOCATION <y>
                        <SUBSET/EXCEPT/FOR qualification>
where <y> is the response variable;
            <stat> is one of H10, H12, H15, H17, H20;
            <par> is a parameter where the computed location value is saved;
and where the <SUBSET/EXCEPT/FOR qualification> is optional.

LET <par> = <stat> SCALE <y>
                        <SUBSET/EXCEPT/FOR qualification>
where <y> is the response variable;
            <stat> is one of H10, H12, H15, H17, H20;
            <par> is a parameter where the computed scale value is saved;
and where the <SUBSET/EXCEPT/FOR qualification> is optional.

LET ALOC = H15 LOCATION Y
LET ASCALE = H15 SCALE Y
LET ALOC = H15 LOCATION Y SUBSET Y > 0
LET ALOC = H20 LOCATION Y

Dataplot uses the Ripley algorithm to compute these statistics.

This method is referred to as Algorithm A in the ISO 13528 standard. The description of the algorithm is taken from that standard.

Dataplot statistics can be used in a number of commands. For details, enter
HELP STATISTICS

None

None

MEAN	= Compute the mean of a variable.
MEDIAN	= Compute the median of a variable.
RANGE	= Compute the range of a variable.
VARIANCE	= Compute the variance of a variable.
STANDARD DEVIATION	= Compute the standard deviation of a variable.
MAD	= Compute the median absolute deviation of a variable.
HOMOSCEDASTICITY PLOT	= Generate a homoscedasticity plot.

Data Analysis, Proficiency Analysis

Analytical Methods Committee, "Robust Statistics--How Not to Reject Outliers: Part 1. Basic Concepts", Analyst, December 1989, Vol. 1.

ISO 13528 (2005), "Statistical Methods for use in proficiency testing by interlaboratory comparisons," Section C.2 Algorithm S.

2010/12

 
SKIP 25
READ GEAR.DAT Y X
LET A = H15 LOCATION Y
.
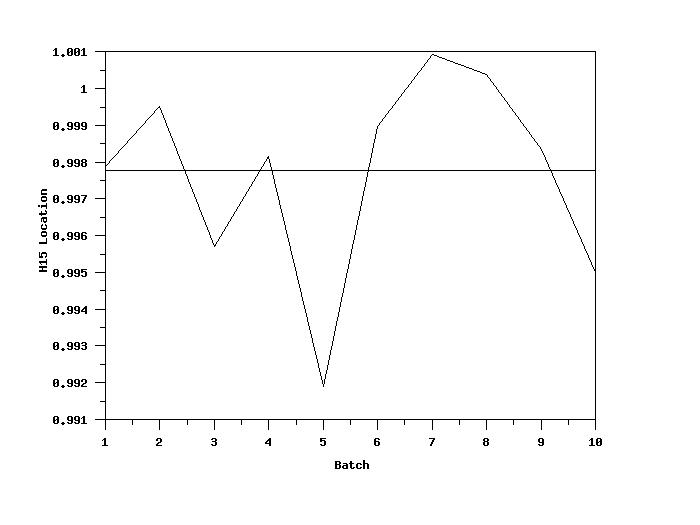
LABEL CASE ASIS
Y1LABEL H15 Location
X1LABEL Batch
H15 LOCATION PLOT Y X
.
LET A = H15 LOCATION Y
SET WRITE DECIMALS 4
SET LET CROSS TABULATE COLLAPSE
LET XGROUP = CROSS TABULATE GROUP ONE X
LET YMEAN = CROSS TABULATE H15 LOCATION Y X
LET YSD   = CROSS TABULATE H15 SCALE    Y X
PRINT XGROUP YMEAN YSD
    

The following output is generated.

---------------------------------------------
         XGROUP          YMEAN            YSD
---------------------------------------------
         1.0000         0.9978         0.0046
         2.0000         0.9995         0.0048
         3.0000         0.9957         0.0037
         4.0000         0.9981         0.0042
         5.0000         0.9919         0.0085
         6.0000         0.9989         0.0108
         7.0000         1.0009         0.0075
         8.0000         1.0003         0.0041
         9.0000         0.9983         0.0045
        10.0000         0.9950         0.0046