MATPDF
Name:
Type:
Purpose:
Compute the classical matching probability mass function.
Description:
The classical matching distribution has the following
probability mass function:
with k a non-negative integer denoting the number of
items parameter.
Given k items numbered 1, 2, ..., k that are
arranged in a random order, the classical matching distribution
is the distribution of the number of items were the original
numbering and the random ordering are the same.
Feller (see References below) formulates this as
the problem where we have two matching decks of cards
and we want to determine the probability of matching
X cards in the two decks.
Syntax:
LET <y> = MATPDF(<x>,<k>)
<SUBSET/EXCEPT/FOR qualification>
where <x> is a variable, a number, or a parameter containing
values between 0 and <k>;
<k> is a number or parameter that defines the upper
limit of the matching distribution;
<y> is a variable or a parameter (depending on what
<x> is) where the computed pdf value is stored;
and where the <SUBSET/EXCEPT/FOR qualification> is optional.
Examples:
LET A = MATPDF(3,20)
LET Y = MATPDF(X,100)
Note:
For a number of commands utilizing the matching distribution,
it is convenient to bin the data. There are two basic ways of
binning the data.
- For some commands (histograms, maximum likelihood
estimation), bins with equal size widths are required.
This can be accomplished with the following commands:
LET AMIN = MINIMUM Y
LET AMAX = MAXIMUM Y
LET AMIN2 = AMIN - 0.5
LET AMAX2 = AMAX + 0.5
CLASS MINIMUM AMIN2
CLASS MAXIMUM AMAX2
CLASS WIDTH 1
LET Y2 X2 = BINNED
- For some commands, unequal width bins may be
helpful. In particular, for the chi-square goodness
of fit, it is typically recommended that the minimum
class frequency be at least 5. In this case, it may
be helpful to combine small frequencies in the tails.
Unequal class width bins can be created with the
commands
LET MINSIZE = <value>
LET Y3 XLOW XHIGH = INTEGER FREQUENCY TABLE Y
If you already have equal width bins data, you can
use the commands
LET MINSIZE = <value>
LET Y3 XLOW XHIGH = COMBINE FREQUENCY TABLE Y2 X2
The MINSIZE parameter defines the minimum class
frequency. The default value is 5.
Note:
You can generate matching random numbers, probability plots,
and chi-square goodness of fit tests with the following commands:
LET N = VALUE
LET K = <value>
LET Y = MATCHING RANDOM NUMBERS FOR I = 1 1 N
MATCHING PROBABILITY PLOT Y
MATCHING PROBABILITY PLOT Y2 X2
MATCHING PROBABILITY PLOT Y3 XLOW XHIGH
MATCHING CHI-SQUARE GOODNESS OF FIT Y
MATCHING CHI-SQUARE GOODNESS OF FIT Y2 X2
MATCHING CHI-SQUARE GOODNESS OF FIT Y3 XLOW XHIGH
Dataplot does not provide any explicit parameter estimation
methods. It is assummed that the number of objects is a
known quantity. We can then apply goodness of fit tests
(i.e., the probability plot or the chi-square goodness of fit)
to see if the classical matching distribution is an appropriate
distribution.
Note:
For sufficiently large values of k, the classical
matching distribution can be accurately approximated with a
Poisson distribution with
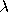 = 1.
Dataplot computes MATPDF from the above definition for values
of k < 20. For values of k ≥ 20, Dataplot
computes MATPDF using the Poisson pdf with = 1.
Dataplot computes MATPDF from the above definition for values
of k < 20. For values of k ≥ 20, Dataplot
computes MATPDF using the Poisson pdf with
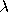 = 1. = 1.
Default:
Synonyms:
Related Commands:
|
MATCDF
|
= Compute the matching cumulative distribution function.
|
|
MATPPF
|
= Compute the matching percent point function.
|
|
POIPDF
|
= Compute the Poisson probability density function.
|
|
LCTPDF
|
= Compute the leads in coin tossing probability mass
function.
|
|
DISPDF
|
= Compute the discrete uniform probability mass function.
|
|
LOSPDF
|
= Compute the lost games probability mass function.
|
|
ARSPDF
|
= Compute the arcsine probability density function.
|
|
BETPDF
|
= Compute the beta probability density function.
|
|
UNIPDF
|
= Compute the uniform probability mass function.
|
Reference:
Johnson, Kotz, and Kemp (1992), "Univariate Discrete
Distributions", Second Edition, Wiley, pp. 409-410.
Feller (1957), "Introduction to Probability Theory",
Third Edition, John Wiley and Sons, pp. 107-109.
Applications:
Implementation Date:
Program:
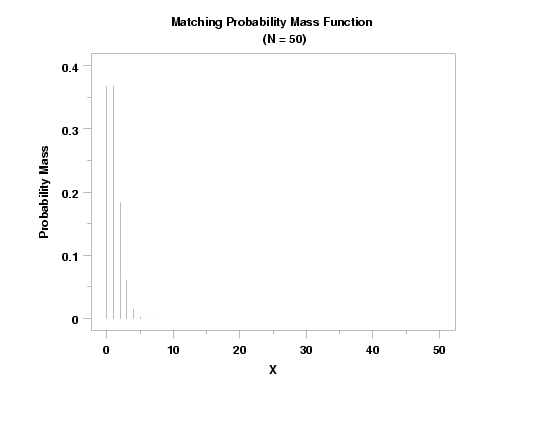
TITLE CASE ASIS
TITLE Matching Probability Mass Function CR() ...
(N = 50)
LABEL CASE ASIS
Y1LABEL Probability Mass
X1LABEL X
LINE BLANK
SPIKE ON
TIC OFFSET UNITS SCREEN
TIC OFFSET 3 3
PLOT MATPDF(X,50) FOR X = 0 1 50
Date created: 6/20/2006
Last updated: 6/20/2006
Please email comments on this WWW page to
alan.heckert@nist.gov.
|


![p(x;k) = (1/x!)*SUM[i=1 to k-x][(-1)^i/i!] x = 0, 1, 2, ..., k](eqns/matpdf.gif)
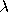 = 1.
Dataplot computes MATPDF from the above definition for values
of k < 20. For values of k ≥ 20, Dataplot
computes MATPDF using the Poisson pdf with
= 1.
Dataplot computes MATPDF from the above definition for values
of k < 20. For values of k ≥ 20, Dataplot
computes MATPDF using the Poisson pdf with
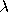 = 1.
= 1.
