SED navigation bar go to SED home page go to Dataplot home page go to NIST home page SED Home Page SED Staff SED Projects SED Products and Publications Search SED Pages
Dataplot Vol 2 Vol 1

MATPPF

Name:
    MATPPF (LET)
Type:
    Library Function
Purpose:
    Compute the classical matching percent point function.
Description:
    The classical matching distribution has the following probability mass function:

      p(x;k) = (1/x!)*SUM[i=1 to k-x][(-1)^i/i!] x = 0, 1, 2, ..., k

    with k a non-negative integer denoting the number of items parameter.

    The cumulative distribution function is computed by summing the probability mass function. The percent point function is the inverse of the cumulative distribution function and is obtained by computing the cumulative distribution function until the specified probability is reached.

Syntax:
    LET <y> = MATPPF(<P>,<k>)             <SUBSET/EXCEPT/FOR qualification>
    where <P> is a variable, a number, or a parameter containing values in the interval (0,1);             <k> is a number or parameter that defines the upper limit of the matching distribution;
                <y> is a variable or a parameter (depending on what <p> is) where the computed ppf value is stored;
    and where the <SUBSET/EXCEPT/FOR qualification> is optional.
Examples:
    LET A = MATPPF(0.95,20)
    LET Y = MATPPF(X,100)
Note:
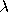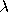    For sufficiently large values of k, the classical matching distribution can be accurately approximated with a Poisson distribution with lambda = 1. Dataplot computes MATPPF from the above definition for values of k < 20. For values of k ≥ 20, Dataplot computes MATPPF using the Poisson pdf with lambda = 1.
Default:
    None
Synonyms:
    None
Related Commands:
    MATCDF = Compute the matching cumulative distribution function.
    MATPDF = Compute the matching probability mass function.
    POIPDF = Compute the Poisson probability density function.
    LCTPDF = Compute the leads in coin tossing probability mass function.
    DISPDF = Compute the discrete uniform probability mass function.
    LOSPDF = Compute the lost games probability mass function.
    ARSPDF = Compute the arcsine probability density function.
    BETPDF = Compute the beta probability density function.
    UNIPDF = Compute the uniform probability mass function.
Reference:
    Johnson, Kotz, and Kemp (1992), "Univariate Discrete Distributions", Second Edition, Wiley, pp. 409-410.

    Feller (1957), "Introduction to Probability Theory", Third Edition, John Wiley and Sons, pp. 107-109.

Applications:
    Distributional Modeling
Implementation Date:
    2006/6
Program: 
     
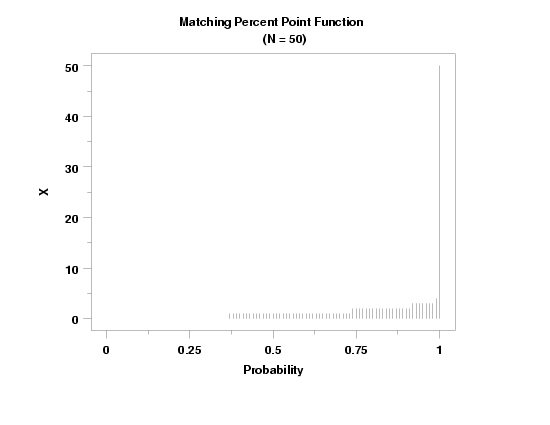
TITLE CASE ASIS
TITLE Matching Percent Point Function CR() ...
      (N = 50)
LABEL CASE ASIS
X1LABEL Probability
Y1LABEL X
LINE BLANK
SPIKE ON
TIC OFFSET UNITS SCREEN
TIC OFFSET 3 3
PLOT MATPPF(P,50) FOR P = 0  0.01  1
    plot generated by sample program

Date created: 6/20/2006
Last updated: 6/20/2006
Please email comments on this WWW page to [email protected].