

|
RGTCDFName:
 and
and
 . .
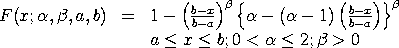
with
The case where a = 0 and b = 1 is referred to as the standard reflected generalized Topp and Leone distribution. It has the following cumulative distribution function:
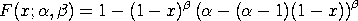
The lower and upper limits are related to the location and scale parameters as follows:
scale = b - a Kotz and van Dorp have proposed this distribution as an alternative to the beta distribution. It is distinguished from the beta distribution in that it can have positive density at the lower limit with a strict positive mode.
<SUBSET/EXCEPT/FOR qualification> where <x> is a number, parameter, or variable containing values in the interval (a,b); <y> is a variable or a parameter (depending on what <x> is) where the computed reflected generalized Topp and Leone cdf value is stored; <alpha> is a number, parameter, or variable in the interval (0, 2) that specifies the first shape parameter; <beta> is a positive number, parameter, or variable that specifies the second shape parameter; <a> is a number, parameter, or variable that specifies the lower limit; <b> is a number, parameter, or variable that specifies the upper limit; and where the <SUBSET/EXCEPT/FOR qualification> is optional. If <a> and <b> are omitted, they default to 0 and 1, respectively.
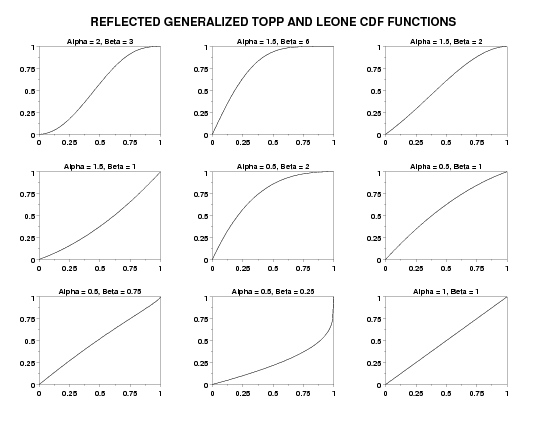
LET Y = RGTCDF(X,0.5,2) PLOT RGTCDF(X,2,3) FOR X = 0 0.01 1
LABEL CASE ASIS
TITLE CASE ASIS
TITLE OFFSET 2
.
MULTIPLOT 3 3
MULTIPLOT CORNER COORDINATES 0 0 100 95
MULTIPLOT SCALE FACTOR 3
.
LET ALPHA = 2
LET BETA = 3
TITLE Alpha = ^alpha, Beta = ^beta
PLOT RGTCDF(X,ALPHA,BETA) FOR X = 0 0.01 1
.
LET ALPHA = 1.5
LET BETA = 6
TITLE Alpha = ^alpha, Beta = ^beta
PLOT RGTCDF(X,ALPHA,BETA) FOR X = 0 0.01 1
.
LET ALPHA = 1.5
LET BETA = 2
TITLE Alpha = ^alpha, Beta = ^beta
PLOT RGTCDF(X,ALPHA,BETA) FOR X = 0 0.01 1
.
LET ALPHA = 1.5
LET BETA = 1
TITLE Alpha = ^alpha, Beta = ^beta
PLOT RGTCDF(X,ALPHA,BETA) FOR X = 0 0.01 1
.
LET ALPHA = 0.5
LET BETA = 2
TITLE Alpha = ^alpha, Beta = ^beta
PLOT RGTCDF(X,ALPHA,BETA) FOR X = 0 0.01 1
.
LET ALPHA = 0.5
LET BETA = 1
TITLE Alpha = ^alpha, Beta = ^beta
PLOT RGTCDF(X,ALPHA,BETA) FOR X = 0 0.01 1
.
LET ALPHA = 0.5
LET BETA = 0.75
TITLE Alpha = ^alpha, Beta = ^beta
PLOT RGTCDF(X,ALPHA,BETA) FOR X = 0 0.01 1
.
LET ALPHA = 0.5
LET BETA = 0.25
TITLE Alpha = ^alpha, Beta = ^beta
PLOT RGTCDF(X,ALPHA,BETA) FOR X = 0 0.01 1
.
LET ALPHA = 1
LET BETA = 1
TITLE Alpha = ^alpha, Beta = ^beta
PLOT RGTCDF(X,ALPHA,BETA) FOR X = 0 0.01 1
.
END OF MULTIPLOT
.
JUSTIFICATION CENTER
MOVE 50 97
TEXT Reflected Generalized Topp and Leone CDF Functions
Date created: 9/10/2007 |