

|
TSSPPFName:
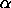 and and
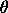 . .
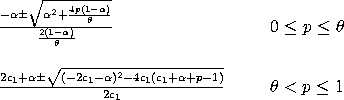
where
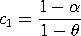
The above equations have two possible roots. The root that lies in the (0,1) interval is the one that is kept. This distribution can be extended with lower and upper bound parameters. If a and b denote the lower and upper bounds, respectively, then the location and scale parameters are:
scale = b - a The general form of the distribution can then be found by using the relation
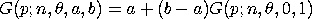
<SUBSET/EXCEPT/FOR qualification> where <p> is a number, parameter, or variable containing values in the interval (0,1); <y> is a variable or a parameter (depending on what <p> is) where the computed two-sided slope ppf value is stored; <alpha> is a number, parameter, or variable in the interval (0,2) that specifies the first shape parameter; <theta> is a number, parameter, or variable in the interval (a,b) that specifies the second shape parameter; <a> is a number, parameter, or variable that specifies the lower bound; <b> is a number, parameter, or variable that specifies the upper bound; and where the <SUBSET/EXCEPT/FOR qualification> is optional. If <a> and <b> are omitted, they default to 0 and 1, respectively.
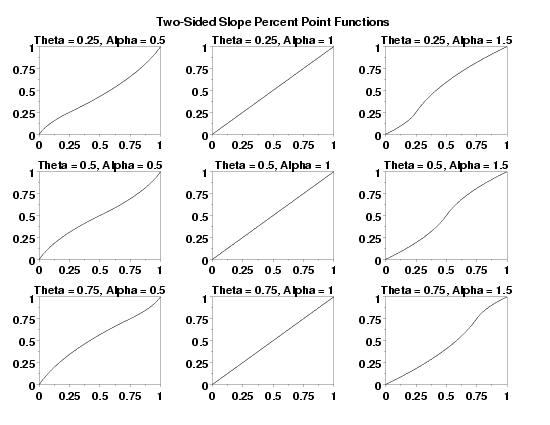
LET Y = TSSPPF(P,1.5,2.2,0,5) PLOT TSSPPF(X,1.5,2.2,0,5) FOR P = 0 0.01 1
MULTIPLOT 3 3
MULTIPLOT CORNER COORDINATES 0 0 100 95
MULTIPLOT SCALE FACTOR 3
TITLE OFFSET 2
TITLE CASE ASIS
LABEL CASE ASIS
CASE ASIS
.
LET THETAV = DATA 0.25 0.50 0.75
LET ALPHAV = DATA 0.5 1.0 1.5
.
LOOP FOR K = 1 1 3
LET THETA = THETAV(K)
LOOP FOR L = 1 1 3
LET ALPHA = ALPHAV(L)
TITLE Theta = ^THETA, Alpha = ^ALPHA
PLOT TSSPPF(P,ALPHA,THETA) FOR P = 0 0.01 1
END OF LOOP
END OF LOOP
.
END OF MULTIPLOT
MOVE 50 97
JUSTIFICATION CENTER
TEXT Two-Sided Slope Percent Point Functions
Date created: 11/07/2007 |