SED navigation bar go to SED home page go to Dataplot home page go to NIST home page SED Home Page SED Staff SED Projects SED Products and Publications Search SED Pages
Dataplot Vol 2 Vol 1

LBEPDF

Name:
    LBEPDF (LET)
Type:
    Library Function
Purpose:
    Compute the log beta probability density function with shape parameters alpha, beta, c, and d.
Description:
    The log beta distribution has the following probability density function:

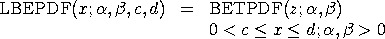
      LBEPDF(x;alpha,beta,c,d) = BETPDF(z;alpha,beta) 0 < c <= x <= d; alpha, beta > 0

    with alpha and beta denoting the shape parameters of the underlying beta distribution, c and d denoting the lower and upper limits of the log beta distribution, BETPDF denoting the beta probability density function, and where

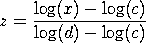
      z = (LOG(x) - LOG(c)/(LOG(d) - LOG(c))

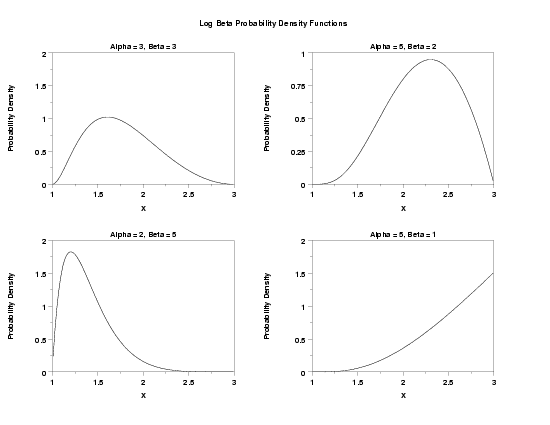
    The log beta distribution has been proposed as an alternative to the log normal distribution. It has the advantage of being able to model both left and right skewness (the lognormal can only model right skewness). It may also be more appropriate when the data has an upper bound.

    The log beta distribution can be generalized with location and scale parameters in the usual way.

Syntax:
    LET <y> = LBEPDF(<y>,<alpha>,<beta>,<c>,<d>,<loc>,<scale>)
                            <SUBSET/EXCEPT/FOR qualification>
    where <x> is a number, parameter, or variable;
                <alpha> is a number, parameter, or variable that specifies the first shape parameter;
                <beta> is a number, parameter, or variable that specifies the second shape parameter;
                <c> is a number, parameter, or variable that specifies the third shape parameter;
                <d> is a number, parameter, or variable that specifies the fourth shape parameter;
                <loc> is a number, parameter, or variable that specifies the optional location parameter;
                <scale> is a number, parameter, or variable that specifies the optional scale parameter;
                <y> is a variable or a parameter (depending on what <x> is) where the computed log beta pdf value is stored;
    and where the <SUBSET/EXCEPT/FOR qualification> is optional.

    The location and scale parameters are optional (the default values are zero and one, respectively).

Examples:
    LET A = LBEPDF(2,6,6,1,3)
    LET Y = LBEPDF(X,ALPHA,BETA,C,D)
    PLOT LBEPDF(X,6,6,1,3) FOR X = 1.01 0.01 2.99
Note:
    Log beta random numbers, probability plots, and goodness of fit tests can be generated with the commands:

      LET ALPHA = <value>
      LET BETA = <value>
      LET C = <value>
      LET D = <value>
      LET Y = LOG BETA RANDOM NUMBERS FOR I = 1 1 N
      LOG BETA PROBABILITY PLOT Y
      LOG BETA PROBABILITY PLOT Y2 X2
      LOG BETA PROBABILITY PLOT Y3 XLOW XHIGH
      LOG BETA KOLMOGOROV SMIRNOV GOODNESS OF FIT Y
      LOG BETA CHI-SQUARE GOODNESS OF FIT Y2 X2
      LOG BETA CHI-SQUARE GOODNESS OF FIT Y3 XLOW XHIGH

    The following commands can be used to estimate the alpha and beta shape parameters (the lower and upper limit parameters c and d are assumed known) for the log beta distribution:

      LET C = <value>
      LET D = <value>
      LET ALPHA1 = <value>
      LET ALPHA2 = <value>
      LET BETA1 = <value>
      LET BETA2 = <value>
      LOG BETA PPCC PLOT Y
      LOG BETA PPCC PLOT Y2 X2
      LOG BETA PPCC PLOT Y3 XLOW XHIGH
      LOG BETA KS PLOT Y
      LOG BETA KS PLOT Y2 X2
      LOG BETA KS PLOT Y3 XLOW XHIGH

    The default values for ALPHA1 and ALPHA2 are 0.5 and 10. The default values for BETA1 and BETA2 are 0.5 and 10.

    Note that the log beta percent point function is expensive to compute. For larger data samples, this can make the above fit commands slow. We can do the following to improve the speed of these commands.

    1. Instead of generating the ppcc plot or ks plot on the original data, we can generate them on selected percentiles of the data. For example, if we have 1,000 points, we can choose to generate the plots on 100 evenly spaced percentiles with the command

        SET PPCC PLOT DATA POINTS 100

    2. For the ks plot, we can speed up the computations considerably by specifying the location and scale parameters with the commands

        LET KSLOC = 0
        LET KSSCALE = 1

      Since this distribution includes the lower and upper limits, location and scale parameters are typically not used.

      The ppcc plot is invariant to location and scale, so there is no speedup obtained by omitting the location and scale parameters.

Default:
    None
Synonyms:
    None
Related Commands:
    LBECDF = Compute the log beta cumulative distribution function.
    LBEPPF = Compute the log beta percent point function.
    BETPDF = Compute the beta probability density function.
    BNOPDF = Compute the beta normal probability density function.
    LGNPDF = Compute the lognormal probability density function.
    PROBABILITY PLOT = Generate a probability plot.
    PPCC PLOT = Generate a ppcc plot.
    KS PLOT = Generate a Kolmogorov-Smirnov (or chi-square for binned data) plot.
    KOLMOGOROV SMIRNOV GOODNESS OF FIT = Perform a Kolmogorov-Smirnov goodness of fit test.
Reference:
    Nadarajah and Gupta (2004). "Applications of the Beta Distribution" in "Handbook of the Beta Distribution", Edited by Gupta and Nadarajah, Marcel-Dekker, pp. 100-102.
Applications:
    Distributional Modeling
Implementation Date:
    2006/8
Program 1: 
     
title displacement 2
y1label displacement 17
x1label displacement 12
case asis
title case asis
label case asis
y1label Probability Density
x1label X
.
let c = 1
let d = 3
.
multiplot corner coordinates 0 0 100 95
multiplot scale factor 2
multiplot 2 2
.
title Alpha = 3, Beta = 3
plot lbepdf(x,3,3,c,d) for x = 1.01  0.01  2.99
.
title Alpha = 5, Beta = 2
plot lbepdf(x,5,2,c,d) for x = 1.01  0.01  2.99
.
title Alpha = 2, Beta = 5
plot lbepdf(x,2,5,c,d) for x = 1.01  0.01  2.99
.
title Alpha = 5, Beta = 1
plot lbepdf(x,5,1,c,d) for x = 1.01  0.01  2.99
.
end of multiplot
.
justification center
move 50 97
text Log Beta Probability Density Functions
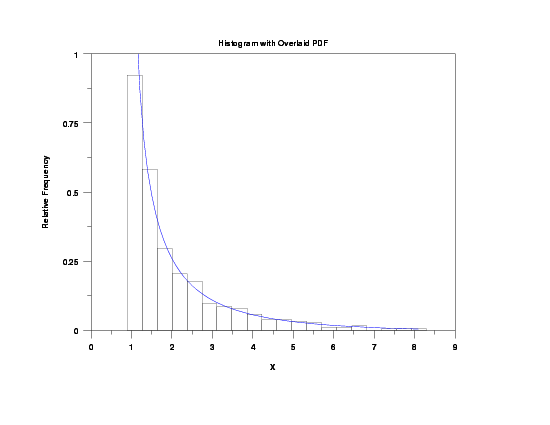
    plot generated by sample program

Program 2: 
     
let alpha = 0.7
let beta = 2.1
let c = 1
let d = 10
let y = log beta rand numb for i = 1 1 500
let y2 x2 = binned y
let amin = minimum y
let amax = maximum y
.
title displacement 2
case asis
title case asis
label case asis
.
title Histogram with Overlaid PDF
y1label Relative Frequency
x1label X
relative histogram y2 x2
limits freeze
pre-erase off
line color blue
plot lbepdf(x,alpha,beta,c,d) for x = amin  0.1  amax
limits
pre-erase on
line color black
.
title Log Beta Probability Plot
y1label Theoretical
x1label Data
char x
line bl
log beta probability plot y
justification center
move 50 6
text PPCC = ^ppcc
line solid
char blank
.
multiplot corner coordinates 0 0 100 100
multiplot scale factor 2
y1label displacement 17
x1label displacement 12
multiplot 2 2
.
let alpha1 = 0.5
let alpha2 = 5
let beta1 = 0.5
let beta2 = 5
set ppcc plot data points 100
.
title PPCC Plot
y1label Correlation Coefficient
x1label Beta (Curves Represent Values of Alpha)
log beta ppcc plot y
let alpha = shape1
let beta  = shape2
set ppcc plot axis order reverse
log beta ppcc plot y
set ppcc plot axis order default
title Probability Plot
y1label Theoretical
x1label Data
log beta probability plot y
log beta kolmogorov smirnov goodness of fit y
title
label
plot
justification left
move 25 90
text Alpha   = ^alpha
move 25 85
text Beta    = ^beta
move 25 80
text PPCC    = ^ppcc
move 25 75
text Min KS  = ^statval
end of multiplot
.
multiplot 2 2
let ksloc = 0
let ksscale = 1
title Chi-Square Plot
y1label Minimum Chi-Square
x1label Beta (Curves Represent Values of Alpha)
log beta ks plot y2 x2
let alpha = shape1
let beta  = shape2
set ppcc plot axis order reverse
log beta ks plot y2 x2
set ppcc plot axis order default
title Probability Plot
y1label Theoretical
x1label Data
log beta probability plot y2 x2
log beta chi-square goodness of fit y2 x2
title
label
plot
justification left
move 25 90
text Alpha   = ^alpha
move 25 85
text Beta    = ^beta
move 25 80
text PPCC    = ^ppcc
move 25 75
text Min KS  = ^statval
end of multiplot
    plot generated by sample program

    plot generated by sample program

    plot generated by sample program 

                       KOLMOGOROV-SMIRNOV GOODNESS-OF-FIT TEST
  
 NULL HYPOTHESIS H0:      DISTRIBUTION FITS THE DATA
 ALTERNATE HYPOTHESIS HA: DISTRIBUTION DOES NOT FIT THE DATA
 DISTRIBUTION:            LOG BETA
    NUMBER OF OBSERVATIONS              =      500
  
 TEST:
 KOLMOGOROV-SMIRNOV TEST STATISTIC      =   0.6439441E-01
  
    ALPHA LEVEL         CUTOFF              CONCLUSION
            10%       0.055*              REJECT H0
                      0.054**
             5%       0.061*              REJECT H0
                      0.060**
             1%       0.073*              ACCEPT H0
                      0.072**
  
     *  - STANDARD LARGE SAMPLE APPROXIMATION  ( C/SQRT(N) )
    ** - MORE ACCURATE LARGE SAMPLE APPROXIMATION  ( C/SQRT(N + SQRT(N/10)) )
    plot generated by sample program 
                       CHI-SQUARED GOODNESS-OF-FIT TEST
  
 NULL HYPOTHESIS H0:      DISTRIBUTION FITS THE DATA
 ALTERNATE HYPOTHESIS HA: DISTRIBUTION DOES NOT FIT THE DATA
 DISTRIBUTION:            LOG BETA
  
 SAMPLE:
    NUMBER OF OBSERVATIONS      =      500
    NUMBER OF NON-EMPTY CELLS   =       20
    NUMBER OF PARAMETERS USED   =        4
  
 TEST:
 CHI-SQUARED TEST STATISTIC     =    6.520930
    DEGREES OF FREEDOM          =       15
    CHI-SQUARED CDF VALUE       =    0.030392
  
    ALPHA LEVEL         CUTOFF              CONCLUSION
            10%       22.30713               ACCEPT H0
             5%       24.99579               ACCEPT H0
             1%       30.57792               ACCEPT H0

Date created: 8/23/2006
Last updated: 8/23/2006
Please email comments on this WWW page to [email protected].