SED navigation bar go to SED home page go to Dataplot home page go to NIST home page SED Home Page SED Staff SED Projects SED Products and Publications Search SED Pages
Dataplot Vol 2 Vol 1

CONPPF

Name:
    CONPPF (LET)
Type:
    Library Function
Purpose:
    Compute the Consul probability mass function.
Description:
    The Consul distribution has the following probability mass function:

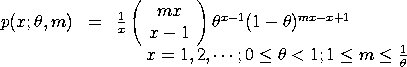
      p(x;theta,m) = (1/x)*(m*x x-1)*theta**(x-1)*(1-theta)**(m*x-x+1) x = 1, ...; 0 < theta < 1; 1 <= m <= 1/theta

    with theta and m denoting the shape parameters. The case where m = 1 reduces to the geometric distribution. For this reason, the Consul distribution is also referred to as the generalized geometric distribution.

    The mean and variance of the Consul distribution are:

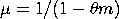
      mu = 1/(1 - theta*m)

      sigma2 = m*theta*(1 - theta)/(1 - m*theta)**3

    The Consul distribution is also parameterized in terms of its mean, mu, which results in the following probability mass function:

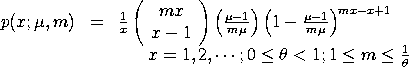
      p(x;mu,m) = (1/x)*(m*x x-1)* ((mu-1)/(m*mu))**(x-1)*(1-(mu-1)/(m*mu))**(m*x-x+1) x = 1, ...; mu > 1; m >= 1

    theta can be expressed in terms of mu:

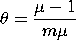
      theta = (mu-1)/(m*mu)

    For this parameterization, the mean and variance are:

      mu

      sigma2 = mu*(mu-1)*(m*mu-mu+1)/m

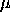
    Dataplot supports both parameterizations (see the Note section below).

    Dataplot computes the cumulative distribution function using the following recurrence relation given on page 320 of Consul and Famoye:

      P(x) = {(m-1)*(x-1) + 1)/(x-1)}*theta*(1-theta)**(m-1)* PROD[i=1 to x-2][1 + m/(m*x-m-i)]*P(x-1)

    where P(1) = (1-theta)**m. If the mu parameterization is used, it is converted to the theta parameterization and the above recurrence relation is applied.

    The Consul percent point function is computed by summing the cumulative distribution function until the specified probability is obtained.

Syntax:
    LET <y> = CONPPF(<p>,<shape>,<m>)
                            <SUBSET/EXCEPT/FOR qualification>
    where <p> is a positive integer variable, number, or parameter in the range (0,1);
                <shape> is a number, parameter, or variable that specifies the valuie of theta (or mu);
                <m> is a number, parameter, or variable that specifies the second shape parameter;
                <y> is a variable or a parameter (depending on what <x> is) where the computed Consul ppf value is stored;
                and where the <SUBSET/EXCEPT/FOR qualification> is optional.
Examples:
    LET A = CONPPF(0.95,0.5,1.4)
    LET Y = CONPPF(P,0.3,1.6)
    PLOT CONPPF(P,0.3,1.6) FOR P = 0 0.01 0.99
Note:
    To use the MU parameterization, enter the command

      SET CONSUL DEFINITION MU

    To restore the THETA parameterization, enter the command

      SET CONSUL DEFINITION THETA
Default:
    None
Synonyms:
    None
Related Commands:
    CONCDF = Compute the Consul cumulative distribution function.
    CONPDF = Compute the Consul probability mass function.
    GEOPDF = Compute the geometric probability mass function.
    GETPDF = Compute the Geeta probability mass function.
    GLSPDF = Compute the generalized logarithmic series probability mass function.
    DLGPDF = Compute the logarithmic series probability mass function.
    YULPDF = Compute the Yule probability mass function.
    ZETPDF = Compute the Zeta probability mass function.
    BGEPDF = Compute the beta geometric probability mass function.
    POIPDF = Compute the Poisson probability mass function.
    BINPDF = Compute the binomial probability mass function.
Reference:
    Consul and Famoye (2006), "Lagrangian Probability Distribution", Birkhauser, chapter 8.

    Famoye (1997), "Generalized Geometric and Some of its Applications", Journal of Mathematical Sciences, 8, pp. 1-13.

    Consul (1990), "New Class of Location-Parameter Discrete Probability Distributions and Their Chaacterizations", Communications in Statistics--Theory and Methods, 19, pp. 4653-4666.

Applications:
    Distributional Modeling
Implementation Date:
    2006/8
Program: 
     
set consul definition theta
title size 3
tic label size 3
label size 3
legend size 3
height 3
x1label displacement 12
y1label displacement 15
.
multiplot corner coordinates 0 0 100 95
multiplot scale factor 2
label case asis
title case asis
case asis
tic offset units screen
tic offset 3 3
title displacement 2
x1label Probability
y1label X
.
xlimits 0 1
major xtic mark number 6
minor xtic mark number 3
.
multiplot 2 2
.
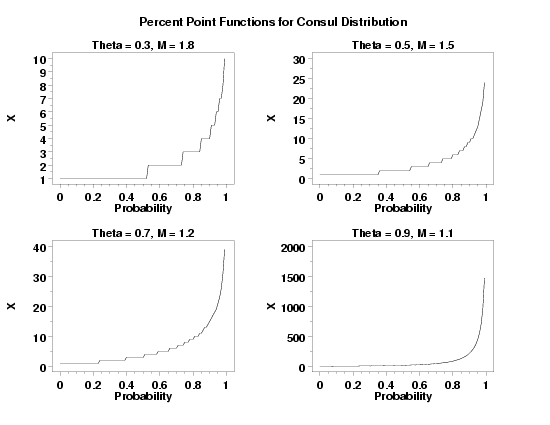
title Theta = 0.3, M = 1.8
plot conppf(p,0.3,1.8) for p = 0  0.01  0.99
.
title Theta = 0.5, M = 1.5
plot conppf(p,0.5,1.5) for p = 0  0.01  0.99
.
title Theta = 0.7, M = 1.2
plot conppf(p,0.7,1.2) for p = 0  0.01  0.99
.
title Theta = 0.9, M = 1.1
plot conppf(p,0.9,1.1) for p = 0  0.01  0.99
.
end of multiplot
.
justification center
move 50 97
text Percent Point Functions for Consul Distribution
    plot generated by sample program

Date created: 8/23/2006
Last updated: 8/23/2006
Please email comments on this WWW page to [email protected].