PERCENTAGE BEND MIDVARIANCE

Name:

PERCENTAGE BEND MIDVARIANCE (LET) Type:

Let Subcommand Purpose:

Compute the percentage bend midvariance for a variable. Description:

resistance means that changing a small part, even by a large amount, of the data does not cause a large change in the estimate
robustness of efficiency means that the statistic has high efficiency in a variety of situations rather than in any one situation. Efficiency means that the estimate is close to optimal estimate given that we know what distribution that the data comes from. A useful measure of efficiency is:

Many statistics have one of these properties. However, it can be difficult to find statistics that are both resistant and have robustness of efficiency.

For scale estimaors, the variance is an optimal estimator for Gaussian data. However, it is not resistant and it does not have robustness of efficiency. The rationale for this estimate is given in these references.

The percentage bend midvariance estimator, discussed in Shoemaker and Hettmansperger and also by Wilcox, is both resistant and robust of efficiency.

The percentage bend midvariance of a a variable X is computed as follows:

Set m = [(1 - \( \beta \) )*n + 0.5]. This is the value of (1 - \( \beta \) )*n + 0.5 rounded down to the nearest integer.
Let W_i = |X_i - M| for i = 1, ..., n where M is the median of X.
Sort the W_i in ascending order.
\( \hat{W}_{x} \) = W(m) (i. e., the m-th order statistic). W(m) is the estimate of the (1-\( \beta \)) quantile of W.
\( Y_i = \frac{X_i - M}{\hat{\omega}_{\beta}} \)
\( A(i) = \log(x_{i}) \)
\( \Psi(x) = \max[-1, \min(1,x)] \)
\( s_{pb} = \frac {n \hat{\omega}_{\beta} \sum_{i=1}^{n}{ \left( \Psi(Y_{i}) \right) ^2} } {(\sum_{i=1}^{n}{a_{i}})^{2} } \)

The value of \( \beta \) is selected between 0 and 0.5. Higher values of \( \beta \) is selected result in a higher breakdown point at the expense of lower efficiency.

Syntax:

Examples:

Note:

LET BETA = <value>

where <value> is greater than 0 and less than or equal to 0.5. The default value for \( \beta \) is 0.1.

Note:

HELP STATISTICS

Default:

None Synonyms:

None Related Commands:

PERCENTAGE BEND CORRELATION	= Compute the percentage bend correlation of a variable.
BIWEIGHT MIDCORRELATION	= Compute a biweight correlation estimate of a variable.
WINSORIZED CORRELATION	= Compute a Winsorized correlation estimate of a variable.
CORRELATION	= Compute the correlation between two variables.
RANK CORRELATION	= Compute the rank correlation between two variables.
VARIANCE	= Compute the variance of a variable.
STATISTIC PLOT	= Generate a statistic versus group plot for a given statistic.

References:

Biometrika 69

Rand Wilcox (1997), "Introduction to Robust Estimation and Hypothesis Testing", Academic Press.

Mosteller and Tukey (1977), "Data Analysis and Regression: A Second Course in Statistics", Addison-Wesley, pp. 203-209.

Applications:

Robust Data Analysis Implementation Date:

2002/07 Program 1:

 
LET Y1 = NORMAL RANDOM NUMBERS FOR I = 1 1 100
LET Y2 = LOGISTIC RANDOM NUMBERS FOR I = 1 1 100
LET Y3 = CAUCHY RANDOM NUMBERS FOR I = 1 1 100
LET Y4 = DOUBLE EXPONENTIAL RANDOM NUMBERS FOR I = 1 1 100
LET A1 = PERCENTAGE BEND MIDVARIANCE Y1
LET A2 = PERCENTAGE BEND MIDVARIANCE Y2
LET A3 = PERCENTAGE BEND MIDVARIANCE Y3
LET A4 = PERCENTAGE BEND MIDVARIANCE Y4

Program 2:

 
MULTIPLOT 2 2
MULTIPLOT CORNER COORDINATES 0 0 100 100
MULTIPLOT SCALE FACTOR 2
X1LABEL DISPLACEMENT 12
.
LET Y1 = NORMAL RANDOM NUMBERS FOR I = 1 1 200
LET Y2 = CAUCHY RANDOM NUMBERS FOR I = 1 1 200
.
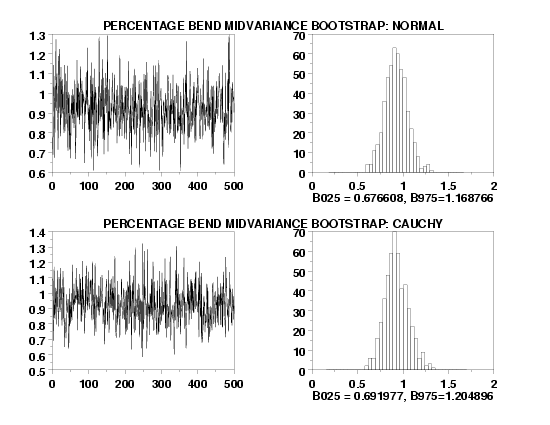
BOOTSTRAP SAMPLES 500
BOOTSTRAP PERCENTAGE BEND MIDVARIANCE PLOT Y1
X1LABEL B025 = ^B025, B975=^B975
HISTOGRAM YPLOT
X1LABEL
.
BOOTSTRAP PERCENTAGE BEND MIDVARIANCE PLOT Y1
X1LABEL B025 = ^B025, B975=^B975
HISTOGRAM YPLOT
.
END OF MULTIPLOT
JUSTIFICATION CENTER
MOVE 50 96
TEXT PERCENTAGE BEND MIDVARIANCE BOOTSTRAP: NORMAL
MOVE 50 46
TEXT PERCENTAGE BEND MIDVARIANCE BOOTSTRAP: CAUCHY