SED navigation bar go to SED home page go to Extreme Winds page go to NIST home page SED Home Page SED Staff SED Projects Extreme Winds Publications Search Wind Pages

Extreme Wind Speeds Software: Excel
Introduction In this section, we provide an example of using Excel to model extreme wind data using a Gumbel distribution.

Note that Excel does not provide some of the sophisticated distributional modeling capabilities that are typically available in statistical programs (e.g., parameter estimation for many different distributions, probability plots for distributions other than the normal, goodness of fit tests, confidence intervals for parameter estimates and quantiles). There are "add-on" programs for Excel that provide more sophisticated statistical capabilities (we do not discuss these other than to mention that they are available). If you have experience writing VBScript macros, you can also implement some of these capabilities by writing your own macros. On the plus side, many engineers and scientists store their data as Excel worksheets, so performing the analysis in Excel can be more convenient.

There are relatively simple estimation procedures for the Gumbel distribution that can be implemented in Excel in a straightforward manner, so we will focus on those in this section. If you want to model extreme wind data using a generalized Pareto, reverse Weibull, extreme value type II (Frechet) or generalized extreme value distribution, we recommend you investigate some of the Excel add-on software that provides more advanced statistical capabilities.

We also provide links to a number of Excel spreadsheets that perform a similar analysis.

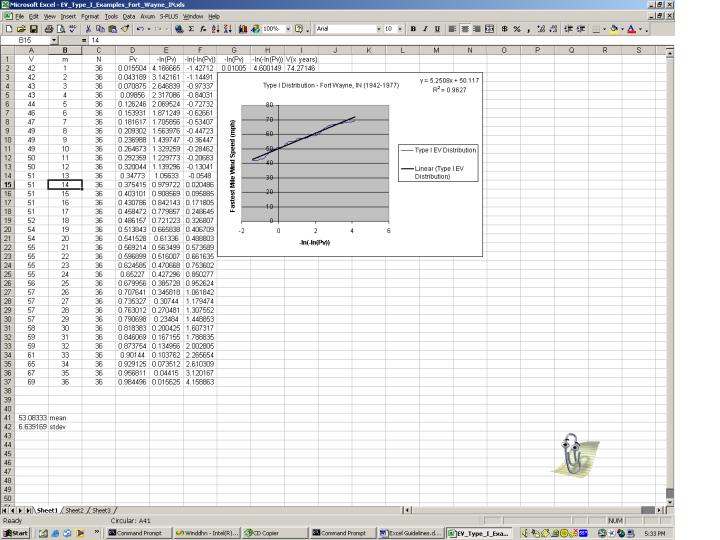
Example: Fort Wayne, IN Below is a snapshot of an Excel worksheet containing annual maximum wind speeds for Fort Wayne, IN for the years 1942-1977. See below for the source and background for this data set.

The worksheet contains the following columns:

  1. V = maximum annual wind speeds in miles per hour (sorted from lowest maximum to highest maximum)
  2. m = rank of the wind speeds from lowest to highest
  3. N = total number of annual maximum observations
  4. Pv = (m - 0.44)/(N + 0.12)
  5. -ln(Pv) = negative of the natural logarithm of Pv (Gringorten Estimation)
  6. -ln(-ln(Pv)) = negative of the natural logarithm of Pv, taken twice
Note that V contains the data that was imported into Excel. The remaining columns were computed in Excel. This data is originally from Simiu, Changery, and Filliben (1979), "Extreme Wind Speeds at 129 Stations in the Contiguous United States," NBS Building Science Series 118 (BSS 118).
Snapshot of Fort Wayne, IN Excel work sheet
Data for Example in HTML Table For clarity, we print the data in the above table as an HTML table.

Table 1: Annual Maximum Wind Speeds for Fort Wayne, IN (1942-1977)
V m N Pv -ln(Pv) -ln(-ln(Pv))
42 1 36 0.015504 4.166665 -1.42712
42 2 36 0.043189 3.142161 -1.14491
43 3 36 0.070875 2.646839 -0.97337
43 4 36 0.09856 2.317086 -0.84031
44 5 36 0.126246 2.069524 -0.72732
46 6 36 0.153931 1.871249 -0.62661
47 7 36 0.181617 1.705856 -0.53407
49 8 36 0.209302 1.563976 -0.44723
49 9 36 0.236988 1.439747 -0.36447
49 10 36 0.264673 1.329259 -0.28462
50 11 36 0.292359 1.229773 -0.20683
50 12 36 0.320044 1.139296 -0.13041
51 13 36 0.34773 1.05633 -0.0548
51 14 36 0.375415 0.979722 0.020486
51 15 36 0.403101 0.908569 0.095885
51 16 36 0.430786 0.842143 0.171805
51 17 36 0.458472 0.779857 0.248645
52 18 36 0.486157 0.721223 0.326807
54 19 36 0.513843 0.665838 0.406709
54 20 36 0.541528 0.61336 0.488803
55 21 36 0.569214 0.563499 0.573589
55 22 36 0.596899 0.516007 0.661635
55 23 36 0.624585 0.470668 0.753602
55 24 36 0.65227 0.427296 0.850277
56 25 36 0.679956 0.385728 0.952624
57 26 36 0.707641 0.345818 1.061842
57 27 36 0.735327 0.30744 1.179474
57 28 36 0.763012 0.270481 1.307552
57 29 36 0.790698 0.23484 1.448853
58 30 36 0.818383 0.200425 1.607317
59 31 36 0.846069 0.167155 1.788835
59 32 36 0.873754 0.134956 2.002805
61 33 36 0.90144 0.103762 2.265654
65 34 36 0.929125 0.073512 2.610309
67 35 36 0.956811 0.04415 3.120167
69 36 36 0.984496 0.015625 4.158863

Worksheet Computations
Sort the Data Once the maximum annual wind speeds were entered into the Excel spreadsheet, they need to be sorted in ascending order from the smallest to the largest. This can be accomplished in Excel by selecting the "Data" button on the toolbar at the top of the page. Then select the "Sort" button in the "Data" menu (this is the first option in the menu). If there is data next to the wind speeds, selecting the "Sort" button results in a "Sort Warning." Select "Continue with Current Selection." After this is selected (or if there is no data next to the wind speed column), the sort menu will appear. Select (if not selected already) Sort by V, select "ascending" and then click the "OK" button. At this point, Excel will properly sort the data.
Creating the Ranks Column The ranks, or m column can be created by first typing a "1" into the m column next to the first annual maximum wind speed. Next, select "1" and drag the cursor down from the "1" in the new column down the cell in the column that is is directly next to the final annual maxima in the data set. Then select "Edit" in the toolbox at the top of the screen. From the "Edit" menu, select the "Fill" command and once in the Fill menu select "Series." Once in the "Series" box, have the "Series in" columns, of the linear "Type" and with "Step Value" of 1. Set "Stop Value" to the same number as the number of annual maxima in the respective data set (36 in this example).
Creating the N Column The number of annual maxima, or N column, is created by first typing the number of annual maxima (36 in our example) into the N column next to the m column. Select this number and then go to the "Edit" toolbar and select "Copy." Next, drag the cursor down from the "36" (or whatever the number happens to be for your data set) in the new column down the cell in the column that is directly next to the final number (36 in this example) in the m column. Go to the "Edit" menu a second time and select "Paste." The column is created.
Creating the Pv, -ln(Pv), and -ln(-ln(Pv)) Columns The next step in creating this worksheet is to create equations to solve Pv (the Gringorten estimation of probability). In Excel, create a new column entitled "Pv". Select cell "D2" (or the first cell in the column that is being used). Select the "fx" box above. An equal sign will appear. From this point, type the equation as shown in Step 1 except:
    m = B2 (or first cell number in m column)
    N = C2 (or first cell number in N column)
So in the "fx" box it should look like:
    fx = (B2-0.44)/(C2+0.12)
This is now the first value in the Pv column. To obtain the remaining values, select the first value, drag down so the Pv column is selected down to the number of N values (36 in our example). Select "Edit", then select "Fill", and finally select "Down." This will add calculated values for the remaining Pv values.

A similar procedure can be followed to create the -ln(Pv) and the -ln(-ln(Pv) columns (note that "ln" is the command for the natural log).

Once the data has been created in the columns, the next step is to graph and fit the data.
Graph the Data
Graph V versus -ln(-ln(Pv)) Graph V versus ln(-ln(Pv)). If the data can be reasonably approximated by a Gumbel distribution, this graph should be approximately linear. If the graph is not approximately linear, this indicates that the Gumbel distribution is not an appropriate distributional model for the data.

Note that this is essentially a probability plot with V denoting the quantiles of the data and ln(-ln(Pv)) denoting the quantiles of the theoretical Gumbel distribution. The theoretical quantiles are obtained by computing the Gumbel percent point (or inverse cumulative distribution) function on the Pv values.

To generate this graph, make sure that no value in any column is selected. Then select the graph icon on the toolbar (blue, yellow, and red bars).

  1. The Chart Wizard will appear. Select XY (Scatter) chart and choose the second chart down and on the left as the chart sub-type. Then click "Next."

  2. Go the the "Series" tab and select "Add" from the Series box. Then click on the far right square in the "X Values" box. This will enable the selection of data from the spreadsheet. Select the first value in the -ln(-ln(Pv) column and drag down to the last value. Once this is finished, select the far right box again. The "X Values" have now been selected. Repeat this procedure for the "Y Values" using the V, the wind speed, column. Name the graph and click "Next."

  3. Write in a title and X and Y axis labels for the chart and click "Next."

  4. Click "Finish." The graph should now be displayed.
Fit the Data
Estimates for Location and Scale The estimates of the location and scale parameters can be obtained by fitting a line to the points on the plot. The slope is an estimate of the scale parameter and the intercept is an estimate of the location parameter.

In Excel, this fitting can be performed by right clicking on the newly created chart and selecting "Add Trendline."

In the "Type" tab, select Linear and under the "Options" tab check to display the equation and the R2 on the chart. Then click "OK."

Values for the Location, Scale and R2 The spreadsheet now shows the graph of V versus ln(-ln(Pv)) along with the equation for the fitted line. It also shows the R2 value for the fit. R2 is the square of the correlation coeffiicent of the points being fit and provides an indication of how well the data are fit by this linear fit. A value of 0 indicates no correlation and a value of 1 indicates perfect positive correlation.

In the example given here, the intercept (i.e., the estimate of the location parameter) is 50.117 and the slope (i.e., the estimate of the scale parameter) is 5.2058. The R2 value is 0.9627.

Estimate Wind Speeds for a Given Return Period Once you have determined that the Gumbel distribution provides an adequate distributional model and have estimated the location and scale parameters, you can estimate the extreme wind speeds for a given return period, R, using the equation:

    G(1/(1 - 1/R))

with G denoting the percent point (or inverse cumulative distribution) function of the Gumbel distribution. The Gumbel percent point function is

    -ln(-ln(1/p))

with p denoting the desired quantile. That is, from R we compute a desired quantile. We then apply the percent point function to this quantile to determine the maximum wind speed that corresponds to the desired return interval.

For example if you want to know the maximum wind expected in the next 100 years:

    Pv = 1 - (1/100) = 0.99
    -LN(-LN(0.99)) = 74.271.

So for this particular example, the 100-year wind is found to be approximately 74 mph. This computation can be performed for any desired return period.

The following table shows the computations performed by Excel.

    Probabilities and 100 Year Wind Return Periods for Fort Wayne, IN
    -ln(Pv) -ln(-ln(Pv)) V(x years)
    0.01005 4.600149 74.27146
Excel Spreadsheets
NBS Building Science Seris 118 The data for the above example is from Simiu, Changery, and Filliben (1979), "Extreme Wind Speeds at 129 Stations in the Contiguous United States," NBS Building Science Series 118.

Note that in this publication the values for return periods are different from those that have been calculated in these examples. The differences are typically of the order of 1-2% and are due to the different estimation methods being used.

Means and standard deviations have also been calculated for the rounded off values and are located in the Excel spreadsheet.

Links to Excel Spreadsheets The following links are to Excel spreadsheets derived from NBS 118 that contain the data and extreme value type I (Gumbel) estimation for 129 stations across the United States. In hurricane zones, the estimation methods may have to be different from those used for non-hurricane regions (see Simiu and Scanlan, Chapter 3). Some of the locations shown have the indication "Caution - Hurricane Zone" on the graph.

All of the wind speeds used in this analysis have been corrected to represent fastest-mile wind speed at 10 meters above ground level. The ratio of 50-year peak gust to 50-year fastest mile gusts is roughly 1.20.

You can also download all of the files as a single zip file.
[Extreme Winds Home |  SED Home |  Structures Group ]

Date created: 05/06/2005
Last updated: 04/26/2023
 Please email comments on this WWW page to SED_webmaster@nist.gov